Attention-Weighted Federated Deep Reinforcement Learning for Device-to-Device Assisted Heterogeneous Collaborative Edge Caching

下载链接

衣带渐宽终不悔

为伊消得人憔悴~

0x00 Abstract

In order to meet the growing demands for multimedia service access and release the pressure of the core network, edge caching and device-to-device (D2D) communication have been regarded as two promising techniques in next generation mobile networks and beyond.

In this article, based on the flexible trilateral cooperation among user equipment, edge base stations and a cloud server, we propose a D2D- assisted heterogeneous collaborative edge caching framework by jointly optimizing the node selection and cache replace- ment in mobile networks.

Key Words: Edge Caching,D2D, Attention-weighted FL, DRL

0x01 INTRODUCTION

Innovative intelligent applications are highly dependent on the computation, storage and communication resources. The low latency for content access and diverse application requirements may not be satisfied if the contents are fetched from remote data centers (e.g., cloud server).

Mobile edge caching (MEC) has been regarded as a promising technique to relieve the burden of backhaul traffic for network operators.In terms of MEC, two key issues, i.e., node selection and cache replacement, need to be properly investigated.Moreover, some existing learning-based methods require users to send their personal data to the central server, which may cause serious issues of user privacy and security.

We are motivated to exploit the framework design of heterogeneous collaborative edge caching by jointly optimizing the node selection and cache replacement in D2D assisted mobile networks, and consider the flexible trilateral collaboration among UEs, BSs and the cloud server.

• We formulate the joint optimization problem as a Markov decision process (MDP), and propose an attention- weighted federated deep reinforcement learning (AWFDRL) framework to address the problem.

• It uses DQN to address the formulated long-term mixed integer linear programming (LT-MILP) problem

• It employs FL to improve the training process by considering the limited computing capacity as well as the user privacy.

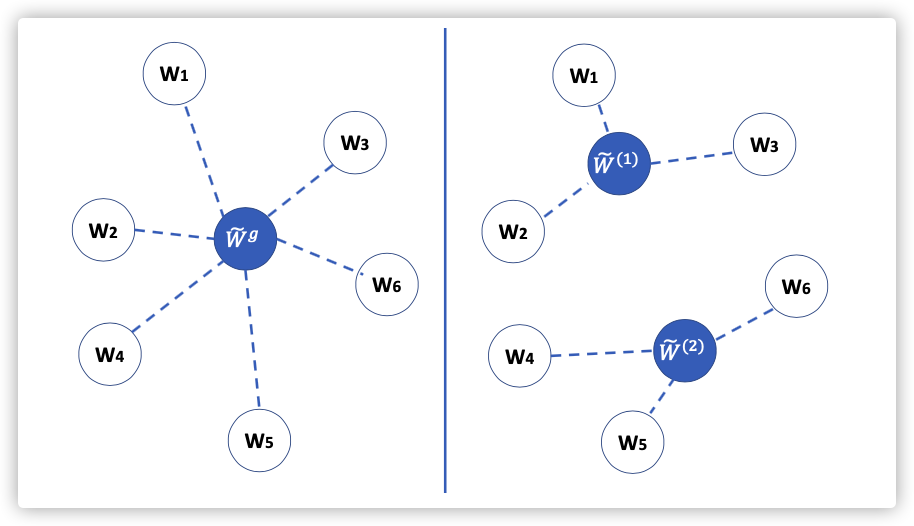
• We employ an attention mechanism to control the model weights in the FL aggregation step, which can address the imbalance issue of local model quality.

  There are many factors that can affect the attention weights and model quality.

  We divide them into three categories as:

  1. user- related factors such as user preference and personal habit;

  2. device-related factors such as CPU capacity and RAM size which may effect the training batch size and replay memory size;

  3. model-related factors such as model staleness and performance loss which can be calculated during the training process.

Note:base stations (BSs) 、user equipment (UE)

0x02 RELATED WORK

0x03 SYSTEM MODEL

A.Network Architecture

• $\mathcal{F}=\{1,2,..,\mathfrak{F}\}$：表示流行的信息,每个数只是信息的id，并不是指信息本身，$s_f$是指其信息$f$大小

• $\mathcal{U}=\{1,2,...,U\}$：用户设备$UE$的索引，$c_u$是指设备可用存储

• $BS_s,BS_n$分别指本地基站和邻居基站

  • 为了简化模型，只考虑一个邻居基站的情况
  • 基站之间通过光纤通信，传输用户请求信息
  • 可用存储是$c_b$

• $Cloud Sever$ 有足够的容量存储$\mathcal{F}$的所有信息，与基站之间是 “backhaul links” 连接

• $x_{u,f},x_{s,f},x_{n,f}=\{0,1\}$ 分别指设备$u$，本地基站$s$,邻居基站$n$有没信息$f$

• $X_u,X_s,X_n$分别指设备$u$，本地基站$s$,邻居基站$n$的缓存状态

B.Content Popularity and User Preference Model

• 利用 MZipf distribution 计算每条信息的流行度：

  $$\omega_f = \frac{(O_f+\tau)^{-\beta}}{\sum_{i\in \mathcal{F}}(O_i+\tau)^{-\beta}},\forall f \in \mathcal{F}$$

  • $O_f$是流行度的倒序排名，$\tau$是高原因数，$\beta$是偏度因子 (防止流行度差距过大的？？)
  • $\Omega=(\omega_f)^{x×\mathfrak{F}}$
  • 假设在一个相对较长的时间内，信息的流行度不会改变

• 用户偏好，用户对信息的请求在其总请求的占比表示其概率：

  $$p_{u}^f = \frac{R_{u,f}}{R_u},\forall u \in \mathcal{U},\forall f \in \mathcal{F}$$

  • $R_{u,f}$表示用户$u$对信息$f$的请求数
  • $\forall u \in \mathcal{U},\sum_{f\in \mathcal{F}}p_u^f=1$

C.D2D Sharing Pattern

从物理维度和社会关系维度分析了用户间的距离，即可能进行信息共享的链路。最终通信图的边是物理维度与社会关系维度的交集。

物理维度：

考虑到信号强度等，只能在用户$u$附近的用户的才可能从$u$获取信息

社会关系维度：

Considering the selfish nature of human beings, mobile users with stronger social relationship are more willing to share their own content directly.

---

emmm，自私自利是人类的天性吗？那为啥不考虑表面笑嘻嘻的假朋友呢？

• 通信图的定义：$\mathcal{G}_C:=\{\mathcal{U},\mathcal{E}_C\},\mathcal{E}_C:=\{(u,v):e^c_{uv}=1\}$

  注：$e^c_{uv}=1$ 表示用户$u,v$既相邻，又是朋友。

• D2D信息共享的概率：利用 tanimoto coefficients计算

  $$r_{uv}^{tan}=\frac{\vec{p_u}\cdot \vec{p_v}}{||\vec{p_u}||^2+||\vec{p_v}||^2-\vec{p_u}\cdot \vec{p_v}},\forall u,v \in \mathcal{U}$$

  • $\forall u \in \mathcal{U},\vec{p_u}=(p_u^f)^{1×\mathfrak{F}}$
  • $for\ pair(u,u),r^{tan}_{uu}:=0$
  • D2D信息共享的概率 $R_{uv}=r_{uv}^{tan}e^c_{uv}$，$\mathbf{R_u}=(R_{uv})^{1×U}$,其中$R$是归一化后的，$R_{uv}=\frac{R_{uv}}{\sum_vR_{uv}}$

D.Content Transmission and Delay Model

$\mathcal{T}=\{1,2,...,T\}$：表示时间段

For each time slot $t ∈ \mathcal{T}$, UE $u$ will send a request $r_{u,t}$ to access a content (say content $f_{u,t}$), and we denote $\mathbf{Req}_t = \{r_{1,t} , r_{2,t} , . . . , r_{U,t} \}$ to describe the request state at time $t$.

对于每个信息的来源会有五种情况，延迟$d$ 会有很大差异，如下图所示，：

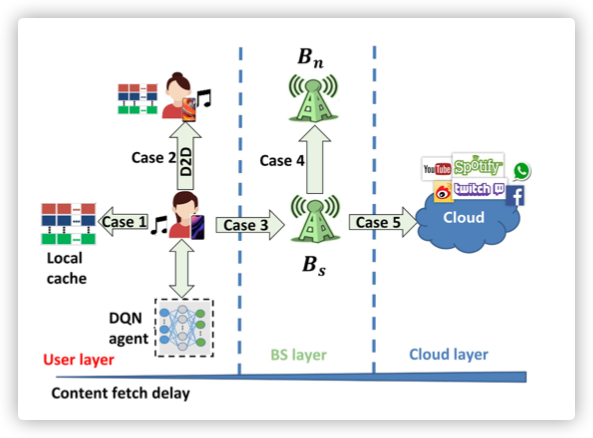
• Case 1: Local cache $d_{u,t}^L:=0$
• Case 2: D2D $d_{u,t}^D:=\frac{s_{f_{u,t}}}{r_{u,t}^D}$
• Case 3: BSs $d_{u,t}^B:=\frac{s_{f_{u,t}}}{r_{u,t}^B}$
• Case 4:BSn $d_{u,t}^{Co}:=d_{u,t}^B+\frac{s_{f_{u,t}}}{r_{u,t}^{Co}}$
• Case5: Cloud $d_{u,t}^{C}:=d_{u,t}^B+\frac{s_{f_{u,t}}}{r_{u,t}^{C}}$

注：此处的 $r_{u,t}^X$ 表示各信道$X$的传输速率

一般有以下的关系：

$$d_{u,t}^L<d_{u,t}^D<d_{u,t}^B<d_{u,t}^{Co}<d_{u,t}^C$$

其实个人感觉基站和D2D之间的关系有点迷。。。可能是书读的太少

0x04 PROBLEM FORMULATION

We formulate the joint problem of node selection and cache replacement in a UE as a Markov deci- sion process (MDP).

A. UE State

$\mathbf{s}_t^u = [\mathbf{\Omega}_t,\vec{p}_u,r_{u,t}^D,\mathbf{X}_u,\mathbf{I}_f]$

$\mathbf{I}_f$ is the indicator on which node caches the requested content $f$.

B.UE Action

UE $u$ decide where to fetch the content through the above methods and which content should be replaced in its cache list.

$\mathbf{a}_t^u = [\beta^f_{u,v,t},\mathbf{X}^f_{u,t}]$

$\beta^f_{u,v,t}$：从哪获取信息，$\mathbf{X}^f_{u,t}$:是否把信息$f$加到缓存队列

C. System Reward

奖励分为D2D网络共享数据量和 信息共享延迟两个方面，前者需要最大化，后者需要最小化.

D2D Sharing Gain:

$$C_{u,t}^1 = \sum_{v \in \mathcal{U}}s_{ f_{u,t} }R_{u,v}x_{v,f}(1-x_{u,f}),\forall u \in \mathcal{U},\forall t \in \mathcal{T}$$

Content Fetch Gain:

$$\begin{aligned} C^2_{u,t}= \left\{ \begin{array}{l} \psi e^{-d^L_{u,t}},\text{Local Cache}\\ \psi e^{-(d_u^Q+d^D_{u,t})},\text{D2D Communication}\\ \psi e^{-d^B_{u,t}},\text{Communication to }B_s\\ \psi e^{-d^{Co}_{u,t}},\text{BS − BS Cooperation}\\ \psi e^{-d^C_{u,t}},\text{Cloud Service}\\ \end{array} \right. \end{aligned}$$

• 其中$d_u^Q$是平均排队等待时间（为多个邻居共享信息，处理不及时，就会有排队情况）
• $\psi$应该是个平衡参数，防止$C^1，C^2$的差距过大（差距过大，较小的那一项就起不到激励函数的作用，可以被砍掉）

System reward

$$C(\mathbf{s}_t^u,\mathbf{a}_t^u) = \lambda_1C^1_{u,t}+\lambda_2C^2_{u,t},\forall u \in \mathcal{U},t \in \mathcal{T}\\ where\ \lambda_1+\lambda_2 = 1,0\leq \lambda_1,\lambda_2 \leq 1$$

D. Value Function

常规的价值函数

0x05 FRAMEWORK DESIGN OF AWFDRL

A. Whole Process

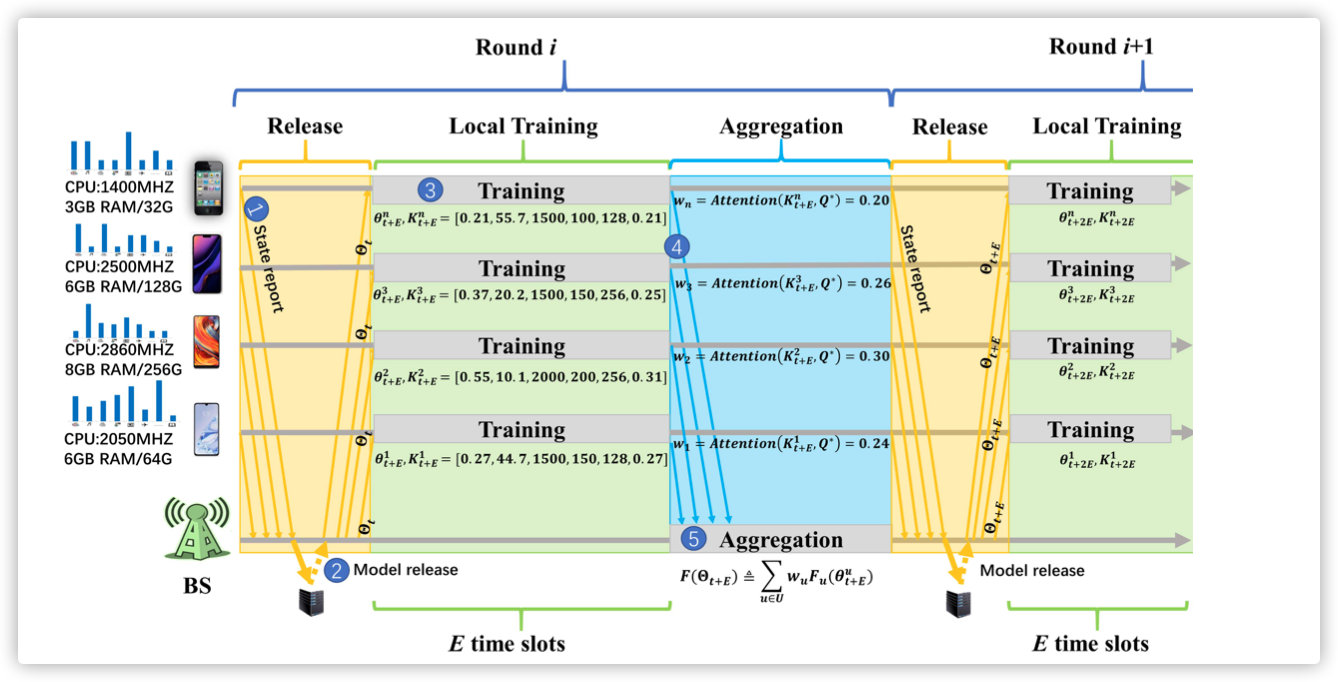
B.Local DQN Model Training

常见的DQN模型

实验中采用的是双层网络架构

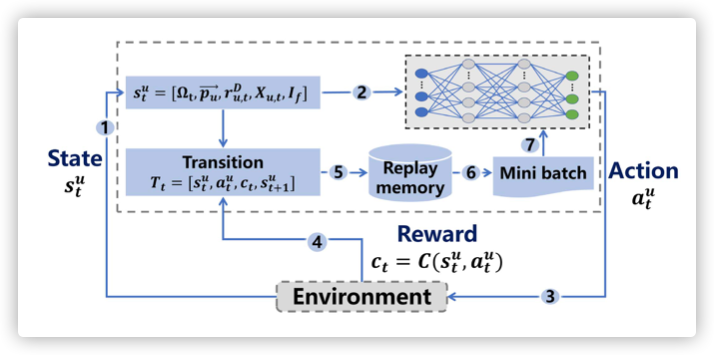
C.Weighted Federated Aggregation

考虑到训练节点的差异性，需要在模型聚合时，确定各模型的权重！

$$\mathop{min}\limits_{\theta,w} \{F(\Theta_t):=\sum_{u\in \mathcal{}U}w_uF_u(\theta^u_t)\}$$

目标：确定$w_u$

方法：Attention

• $\mathbf{K_u}=[\bar{C}_u,\bar{L}_u,M_u,E_u,m_u,\bar{h}_u]$
• $\mathbf{Q}=[max_u(\bar{C}_u),min_u(\bar{L}_u),max_u(M_u),max_u(E_u),max_u(m_u),max_u(\bar{h}_u)]$
• $\mathbf{V_u}:=Model_u$

考虑的信息为:

[Average reward,Average loss,Training data size,Episode number,Batch size,Hit rate]

• 计算方式：

  $$w_u=Attention(\mathbf{Q},\mathbf{K_u})=softmax(\frac{\mathbf{Q}\mathbf{K_u}^T}{\sqrt{d_k}}),\forall u \in \mathcal{U}$$

D. Convergence Analysis

参考：

• MZipf distribution（齐夫定律）
• tanimoto coefficients