参考书籍 邹伟博士的《强化学习》

此篇笔记用于整理知识，因此全部基于个人理解…

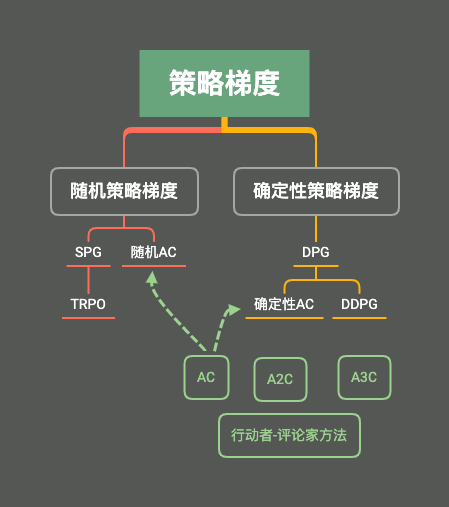
0x08 随机策略梯度

到目前为止，基于值的方法可以在获得最优值的同时获得对应的动作，以此作为最优策略！

随机策略主旨：πθ(a∣s)=p(a∣s,θ)\pi_{\theta}(a|s)=p(a|s,\theta)是输出动作的分布概率，并非准确的动作，基于采样数据更新，而且采样也伴随着随机过程！

所以从当前状态到下一状态存在两个随机过程：动作的选择，状态的转移~

但是存在动作连续(或者数目很大的情况)，argmaxaQ(s,a)argmax_a Q(s,a)就变得不切实际，因此可以直接将策略参数化，利用线性或者非线性函数表示策略，即πθ(s)\pi_{\theta}(s)，以寻求最优的参数θ\theta，使得累计回报的期望E[∑tR(st)∣πθ]E[\sum_t R(s_t)|\pi_{\theta}] 最大，这就是策略搜索方法。

最先发展的策略搜索方法是随机策略梯度，求解最优目标时，采用梯度上升法！(求解最大值)

优缺点及分类

  • 更好的收敛性
  • 更简单的搜索方法
  • 可以学到随机策略
  • 可能收敛到局部最小，学习不够高效！

随机策略梯度定理及证明

  • 对于有终止状态的情况，可以使用累计回报作为目标函数，即：

    J(θ)=Vπθ(s0)J(\theta) = V_{\pi_{\theta}}(s_0)

  • 对于没有终止状态的，考虑一段时间的回报期望作为目标函数，即：

    J(θ)=∑t=1uπθ(s)∑aπθ(a∣s,θ)RsaJ(\theta) = \sum_{t=1}u_{\pi_{\theta}}(s)\sum_{a}\pi_{\theta}(a|s,\theta)R_s^a

    其中uπθ(s)u_{\pi_{\theta}}(s) 是基于策略πθ\pi_{\theta}生成的马尔可夫链关于状态的分布，在分布未知的情况下，就算目标函数对策略参数的梯度十分困难！

    策略梯度定理能很好解决这种问题，并将上述两种情况在理论上统一成一种表示式：

    ∇J(θ)∝∑suπθ(s)∑aQπ(s,a)∇θπθ(a∣s,θ)=∑suπθ(s)∑aπθ(a∣s,θ)Qπ(s,a)∇θπθ(a∣s,θ)πθ(a∣s,θ)=Es∼u,a∼π[Qπ(s,a)∇θπθ(a∣s,θ)πθ(a∣s,θ)]=Es∼u,a∼π[∇θlogπθ(a∣s,θ)Qπ(s,a)]\begin{aligned} \nabla J(\theta) &\propto \sum_su_{\pi_{\theta}}(s)\sum_aQ_{\pi}(s,a)\nabla_{\theta}\pi_{\theta}(a|s,\theta)\\ &=\sum_s u_{\pi_{\theta}}(s) \sum_a\pi_{\theta}(a|s,\theta)Q_{\pi}(s,a)\frac{\nabla_{\theta}\pi_{\theta}(a|s,\theta)}{\pi_{\theta}(a|s,\theta)}\\ &=E_{s\sim u,a\sim \pi}[Q_{\pi}(s,a)\frac{\nabla_{\theta}\pi_{\theta}(a|s,\theta)}{\pi_{\theta}(a|s,\theta)}]\\ &=E_{s\sim u,a\sim \pi}[\nabla_{\theta}log\pi_{\theta}(a|s,\theta)Q_{\pi}(s,a)] \end{aligned}

证明：

有时间再整理~

蒙特卡罗策略梯度

有上式知，需要根据采样at,st→a,sa_t,s_t\to a,s ，又因为Es∼u,a∼π[Gt∣st,at]=Qπ(st,at)E_{s\sim u,a\sim \pi}[G_t|s_t,a_t] = Q_{\pi}(s_t,a_t)所以有:

∇θJ(θ)=Es∼u,a∼π[∇θlogπθ(at∣st,θ)Qπ(st,at)]=Es∼u,a∼π[Gt∇θlogπθ(at∣st,θ)]\nabla_{\theta}J(\theta) =E_{s\sim u,a\sim \pi}[\nabla_{\theta}log\pi_{\theta}(a_t|s_t,\theta)Q_{\pi}(s_t,a_t)]=E_{s\sim u,a\sim \pi}[G_t\nabla_{\theta}log\pi_{\theta}(a_t|s_t,\theta)]

结合梯度上升公式θt+1=θt+α∇J(θt)\theta_{t+1} = \theta_{t} + \alpha\nabla J(\theta_{t})，则有REINFORCE方法:

θt+1=θt+αGt∇θlogπθ(at∣st,θ)\theta_{t+1} = \theta_{t} + \alpha G_t\nabla_{\theta}log\pi_{\theta}(a_t|s_t,\theta)

带基线的REINFORCE方法：

为了减少方差，因此引入基线函数b(s)b(s)，其与动作无关，只与状态相关:

∇J(θ)∝∑suπθ(s)∑a(Qπ(s,a)−b(s))∇θπθ(a∣s,θ)\nabla J(\theta) \propto \sum_su_{\pi_{\theta}}(s)\sum_a(Q_{\pi}(s,a)-b(s))\nabla_{\theta}\pi_{\theta}(a|s,\theta)

而且不会改变梯度本身，其证明如下:

∑suπθ(s)∑ab(s)∇θπθ(a∣s,θ)=∑suπθ(s)b(s)∑a∇θπθ(a∣s,θ)=∑suπθ(s)b(s)∑a∇θ1=0\begin{aligned} & \sum_su_{\pi_{\theta}}(s)\sum_ab(s)\nabla_{\theta}\pi_{\theta}(a|s,\theta)\\ &=\sum_su_{\pi_{\theta}}(s)b(s)\sum_a\nabla_{\theta}\pi_{\theta}(a|s,\theta)\\ &=\sum_su_{\pi_{\theta}}(s)b(s)\sum_a\nabla_{\theta}1\\ &=0 \end{aligned}

TRPO方法

上述方法无法选择一个合适的步长α\alpha，使得学习方法单调收敛~

证明有些复杂~下次一定

0x09 Actor-Critic及变种

Actor-Critic 方法

Actor网络用于选择动作以达到最大的回报，Critic网络用于对动作进行打分，以减少回报估计值和回报真实之间的差距为目标。

训练时，两者同时训练，提升效果，只有好的评委才能指导出好的演员~

训练后，使用的就是Actor网络，根据状态选择动作

对行为值函数Qπ(s,a)Q_{\pi}(s,a)进行参数近似：Qw(s,a)Q_{w}(s,a)，Actor按照Critic得到行为值函数，对参数θ\theta进行更新:

Δθ=α∇θlogπθ(a∣s)Qw(s,a)\Delta \theta = \alpha \nabla_{\theta} log\pi_{\theta}(a|s)Q_{w}(s,a)

  • 使用梯度上升更新Critic网络：

    δ=r+γQw(s′,a′)−Qw(s,a)w=w+βδ∇wQw(s,a)\delta = r + \gamma Q_w(s',a')-Q_w(s,a)\\ w = w + \beta\delta\nabla_wQ_w(s,a)

  • 使用梯度下降更新Actor网络：

    θ=θ+α∇θlogπθ(a∣s)Qw(s,a)\theta = \theta+\alpha \nabla_{\theta} log\pi_{\theta}(a|s)Q_{w}(s,a)

A2C (Advantage AC)方法

与前面介绍的REINFORCE方法一样，引入基线函数减少方差~

理论上基线函数满足只与状态相关即可，这里采用的基线函数B(s)=Vπθ(s)B(s)=V_{\pi_{\theta}}(s)

则优势函数为：Aπθ(s,a)=Qπθ(s,a)−Vπθ(s)A_{\pi_{\theta}}(s,a)=Q_{\pi_{\theta}}(s,a)-V_{\pi_{\theta}}(s)

目标函数的梯度如下：

∇θJ(θ)=Eπθ[∇θlogπθ(a∣s)(Qπθ(s,a)−Vπθ(s))]=Eπθ[∇θlogπθ(a∣s)Aπθ(s,a)]\nabla_{\theta}J(\theta)=E_{\pi_{\theta}}[\nabla_{\theta}log\pi_{\theta}(a|s)(Q_{\pi_{\theta}}(s,a)-V_{\pi_{\theta}}(s))]=E_{\pi_{\theta}}[\nabla_{\theta}log\pi_{\theta}(a|s)A_{\pi_{\theta}}(s,a)]

如果根据上式进行更新，则Critic需要更新两套参数：更新V(s)V(s)一套, 更新Q(s,a)Q(s,a)一套

但在实际操作中，要用TD误差代替优势函数进行计算，因为TD误差是优势函数的无偏估计：

δπθ=r+γVπθ(s′)−Vπθ(s)Eπθ[δπθ∣s,a]=Eπθ[r+γVπθ(s′)∣s,a]−Vπθ(s)=Qπθ(s,a)−Vπθ(s)=Aπθ(s,a)\delta_{\pi_{\theta}} = r+\gamma V_{\pi_{\theta}}(s')-V_{\pi_{\theta}}(s)\\ E_{\pi_{\theta}}[\delta_{\pi_{\theta}}|s,a] = E_{\pi_{\theta}}[r+\gamma V_{\pi_{\theta}}(s')|s,a]-V_{\pi_{\theta}}(s)=Q_{\pi_{\theta}}(s,a)-V_{\pi_{\theta}}(s)=A_{\pi_{\theta}}(s,a)

因此只需要一套参数更新即可：

∇θJ(θ)=Eπθ[∇θlogπθ(a∣s)δπθ]\nabla_{\theta}J(\theta)=E_{\pi_{\theta}}[\nabla_{\theta}log\pi_{\theta}(a|s)\delta_{\pi_{\theta}}]

A3C

多个CPU线程进行异步学习，周期性同步参数~

0x0A 确定性策略梯度

对高纬度的行为空间的采样，和计算高纬度的期望非常复杂~

因此引入确定性策略：给定状态，返回一个动作~ a=μθ(s)a=\mu_{\theta}(s)

确定性策略梯度定理

假设在一个马尔可夫决策模型中，p(s′∣s,a),∇ap(s′∣s,a),μθ(s),∇θμθ(s),r(s,a),∇ar(s,a),p1(s)p(s'|s,a),\nabla_a p(s'|s,a),\mu_{\theta}(s),\nabla_{\theta}\mu_{\theta}(s),r(s,a),\nabla_a r(s,a),p_1(s)分别存在，并且对于s,s′,a,θs,s',a,\theta都是连续函数，(其中p1(s)p_1(s)表示初始状态概率分布函数，p(s′∣s,a)p(s'|s,a)表示状态转移概率，以上条件时为了保证∇θμθ(s)\nabla_{\theta}\mu_{\theta}(s)