Overcoming Noisy and Irrelevant Data in Federated Learning
0x00 Abstract
A challenge is that among the large variety of data collected at each client, it is likely that only a subset is relevant for a learning task while the rest of data has a negative impact on model training.
In this paper, we propose a method for distributedly selecting relevant data, where we use a benchmark model trained on a small benchmark dataset that is task-specific, to evaluate the relevance of individual data samples at each client and select the data with sufficiently high relevance.
Key Words: Federated Learning,Data filtering
0x01 INTRODUCTION
Existing work on federated learning mostly focused on model training using pre-defined datasets at client devices.
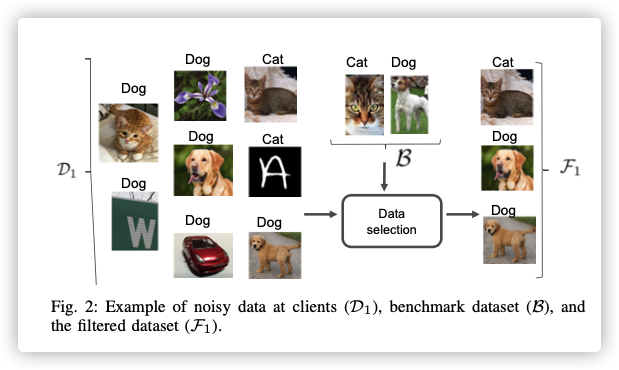
For example, if the task is to classify handwritten digits, printed digits can be considered as irrelevant data although they may be tagged with the same set of labels.Including irrelevant data in the federated learning process can reduce model accuracy and slow down training.
We consider a federated learning system with a model requester (MR), multiple clients, and a server. A federated learning task is defined by the MR which provides the model logic (e.g., a specific deep neural network architecture). The MR can be any user device with computational capability, which may or may not be a client or the server at the same time.
In our proposed approach, the MR has a small set of benchmark data that is used as an example to capture the desired input-output relation of the trained model, but is insufficient to train the model itself.
In this way, our approach works in a distributed manner without requiring clients or MR to share raw data.
0x02 RELATED WORK
It does not allow the more realistic setting where relevant and irrelevant data (with respect to a particular learning task) coexist at each client.
Relevant and irrelevant data in the training dataset has been considered for centralized machine learning in recent years particularly in the domain of image recognition, where irrelevant data can be regarded as noise for a given machine learning task.
Closed-setvs.open-setnoise
Closed-set noise: Data sample of a known class is labeled as another known class.Open-set noise: Data sample of an unknown class is labeled as a known classStrongvs.weaknoise
Strong noise: The number of noisy data samples can exceed the number of clean data samples.Weak noise: The number of noisy data samples is less than the number of clean data samples.
We note that all the approaches that address the strong noise scenario require a small set of clean benchmark data, as we do in our paper.
The problem of filtering out noisy training data is also broadly related to the area of anomaly/outlier detection. However, anomaly detection techniques focus on detecting anomalous data samples based on the underlying distribution of the data itself, instead of how the data impacts model training.
To the best of our knowledge, none of the following aspects has been studied in the literature:
strong open-set noise in training data and its impact on the learning performance,
data cleansing/filtering in federated learning with decentralized datasets located at clients.
We propose a novel method of filtering the data in a distributed manner for federated learning with strong open-set noise, which also works in weak noise and closed-set noise scenarios at the same time.
0x03 SYSTEM MODEL AND DEFINITIONS
The MR specifies what model needs to be trained, and also has
a small benchmark datasetthat can be generated by the MR based on its own knowledge of the learning task or via other means, but are deemed to have correct labels for all data in it.In this paper, we assume that the clients are trusted and cooperative. They voluntarily participate in refining the dataset for each task. The noise in the data (with respect to the task) can be due to the following reasons:
- irrelevance of the data to the task,
- data mislabeling by the client or by a third-party that provides data to the client,
- lack of proper representation of data labels in the system (e.g., a label “0” can represent different things depending on the context).
基础背景:
- 假设总共有个训练节点,每个节点拥有的数据量是,且
- 设每个节点上与目标任务相关的数据集为,且
- 损失函数
对于每个训练的节点的损失值:
对于联邦学习的全局损失:
联邦学习的目标:
对于更新参数使用:
对参数全局聚合:
In this paper, we use a fixed percentage of as the mini-batch size of each client n, thus different clients may have different mini-batch sizes depending on .
0x04 DATA SELECTION
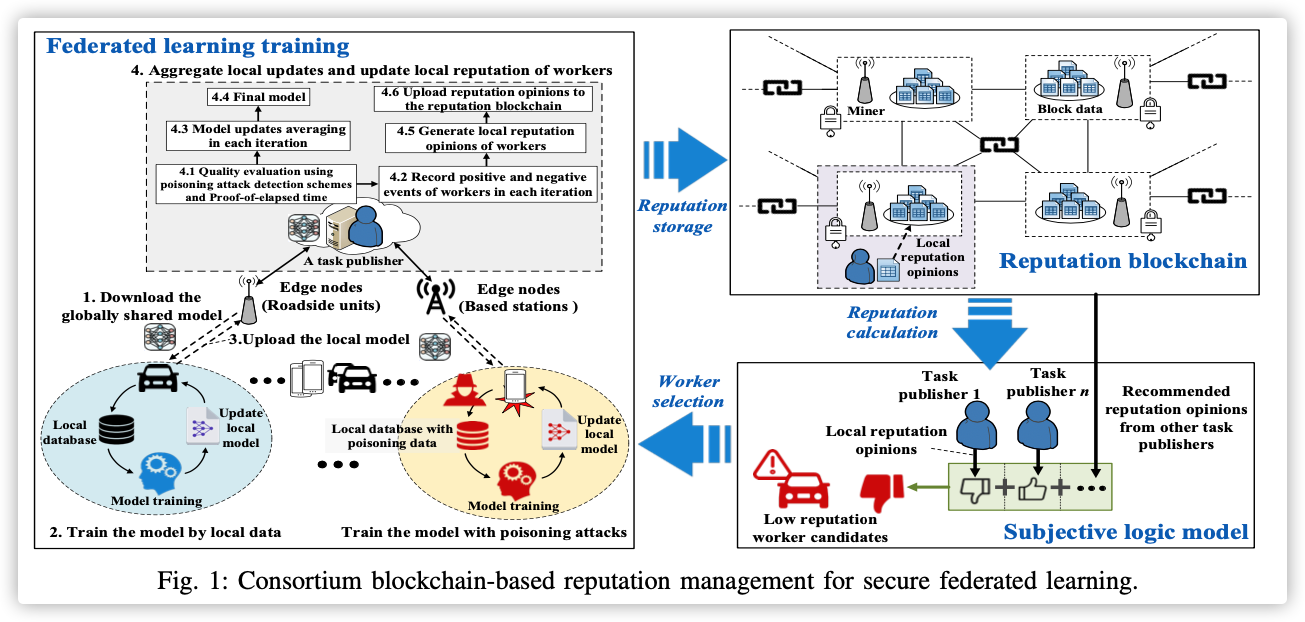
The goal is to filter out noisy data samples to the specific federated learning task. The filtering process is decentralized, where each client performs the filtering operation on its own dataset and only exchanges a small amount of meta-information with the server.
The main idea is that the MR first trains a benchmark model (of the same type as the final model requested by the MR) using only a subset of the benchmark data owned by the MR .
这部分基准数据集是为了帮助确定与训练节点数据集的相关性的。(观点:如果模型预测损失值越大,则test数据与train数据相关性越低)
本文根据辅助数据集与节点数据损失值的分布,确定了一个阈值,数据样本的损失超过该阈值,就被认为是噪声,并且会从训练中除去。
大致流程如下:
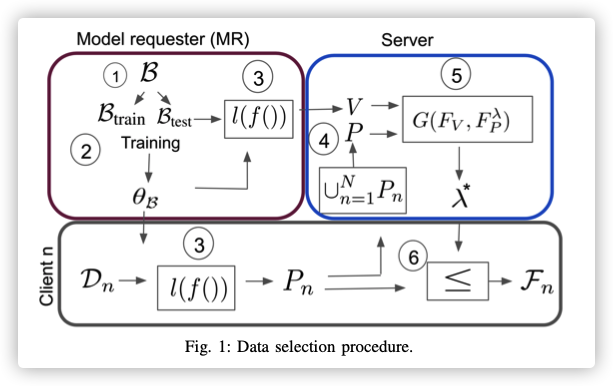
- MR训练一个基准模型(训练数据集都是相关数据集,无噪声),然后在辅助数据集上评估,获得基准损失值分布。
- 每个训练节点,用基准模型评估本地数据集,获得本地损失值分布。
- 服务器收集所有本地损失值分布,并将其与基准损失值的分布相比较,获得筛选阈值。
- 每个训练节点根据该阈值过滤噪声数据样本。
A. Objective
训练目标:模型在测试数据集上的损失最小。
测试数据集是一个辅助数据集,与全局数据集和基准数据集相交均为空。
PS:准确来说是另个一辅助数据集,只是用来检测模型训练程度,与计算基准损失值分布数据集不同!
B. Training Benchmark Model
将基准数据集分成与。
基准模型的训练:
C. Finding Loss Distribution Using Benchmark Model
-
计算的损失值分布:
-
计算各节点数据的损失值分布:
-
假设:越小的损失表示该样本越适合此训练任务。
-
这个假设直观上这样是没错,但是应该也需要考虑基准数据集对基准模型的训练程度吧,会不会出现比较好的数据集,但是损失有点大的问题?
-
这个基准数据集是不是需要囊括所有种类?这个要求高吗?对没遇到的种类,模型又要怎么判断?
-
D. Calculating Filtering Threshold in Loss Values
In other words, we assume that data samples, whose loss values evaluated with the benchmark model are within an “acceptable” range in the distribution of V , have a high probability to be relevant to the learning of the target model.
现在的问题就是怎么合理的确定这阈值?
-
将损失值分布转换成概率分布:
- ,
- 受限分布:
-
使用
Kolmogorov-Smirnov (KS) distance定义两个分布之间的距离: -
最小化,计算最佳阈值:
知识补充:
Kolmogorov-Smirnov distance:
目的:用于检验两个分布是否相似或不同。
过程:
- 将两个分布绘制到同一横轴分布图
0x05 EXPERIMENTATION RESULTS
A. Setup
-
-
DataSet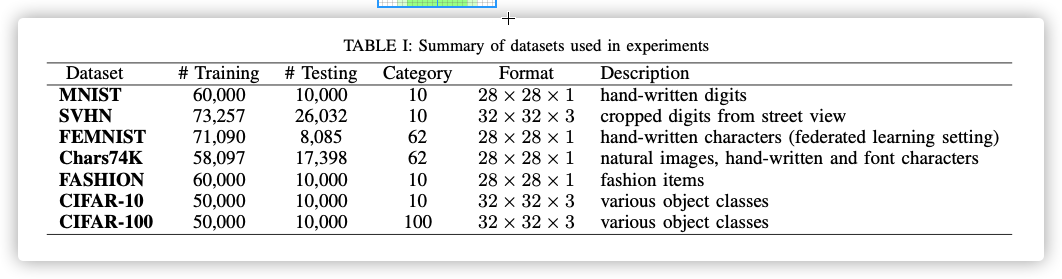
-
Data Partition Among ClientsFor FEMNIST which is already partitioned by the writers, we consider the images from each writer as belonging to a separate client.
For all other datasets, the data are distributed into clients so that each client has only one class (label) of data from that dataset.
The clients and labels are associated randomly, so that the number of clients for each label differ by at most one.
For all clients with the same label, the data with this label are partitioned into clients randomly. When multiple datasets are mixed together (the open-set noise setting), different clients have different proportions of samples from each dataset, resulting in different amount of data samples in total.
We have clients in any experiment involving FEMNIST which is obtained using the default value in FEMNIST for non-i.i.d. partition .
For experiments without FEMNIST, we assume clients.
-
Noisy Data -
Benchmark DataThe benchmark dataset used to build the benchmark model is obtained by sampling a certain percentage of data from the original (clean) datasets.
For all datasets other than FEMNIST, the benchmark dataset is sampled randomly from the training data. For FEMNIST, which is pre-partitioned, the benchmark dataset only includes data from a small subset of partitions (clients) corresponding to individual writers.
-
Model and Baseline Methods-
CNN -
SGD -
Local updates: -
Mini-Batch: -
Baseline MethodsTo evaluate our data selection method, we consider three baseline methods for comparison:
-
Model trained only on the small benchmark dataset (referred to as the benchmark model);
-
Model trained with federated learning using only the target dataset without noise at each client (i.e., the ideal case);
-
Model trained with federated learning using all the (noisy) data at clients without data selection.
-
-
B. Results
-
Data Selection Performance (Different Types of Noise)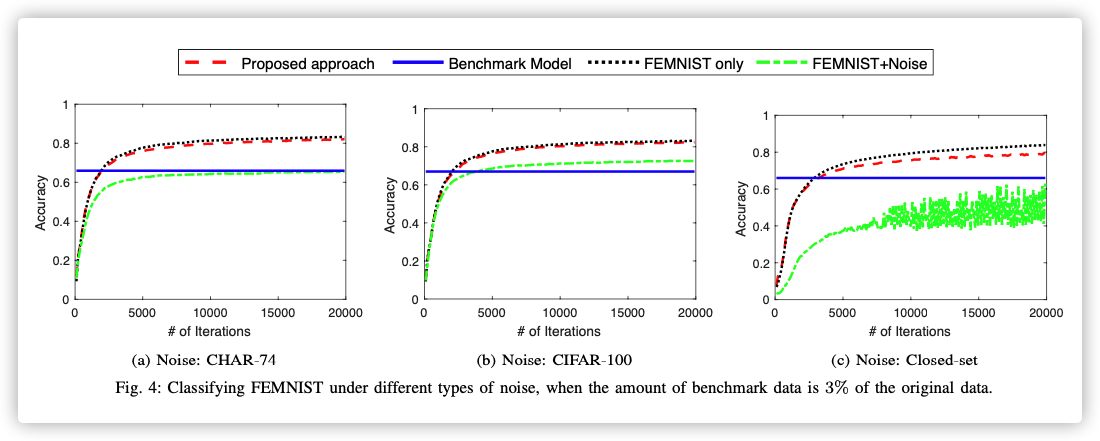
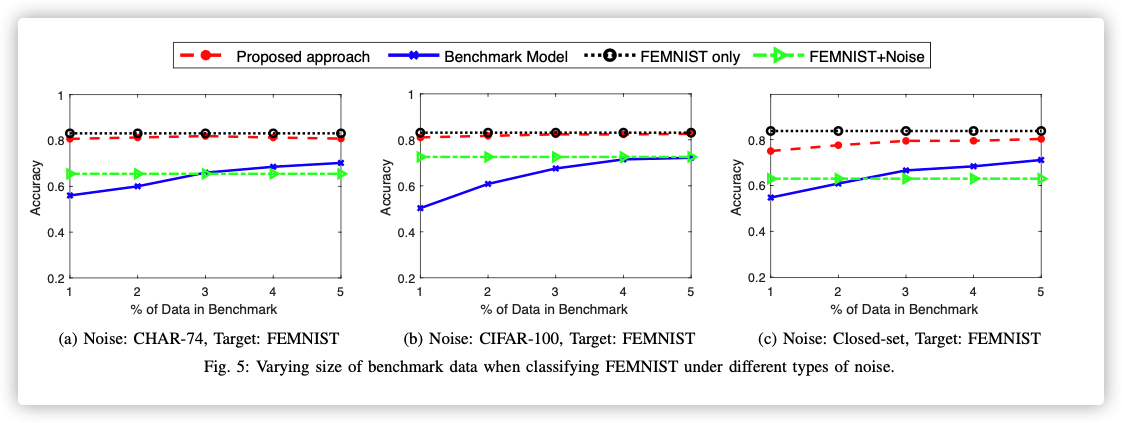
-
Data Selection Performance (Strong Noise)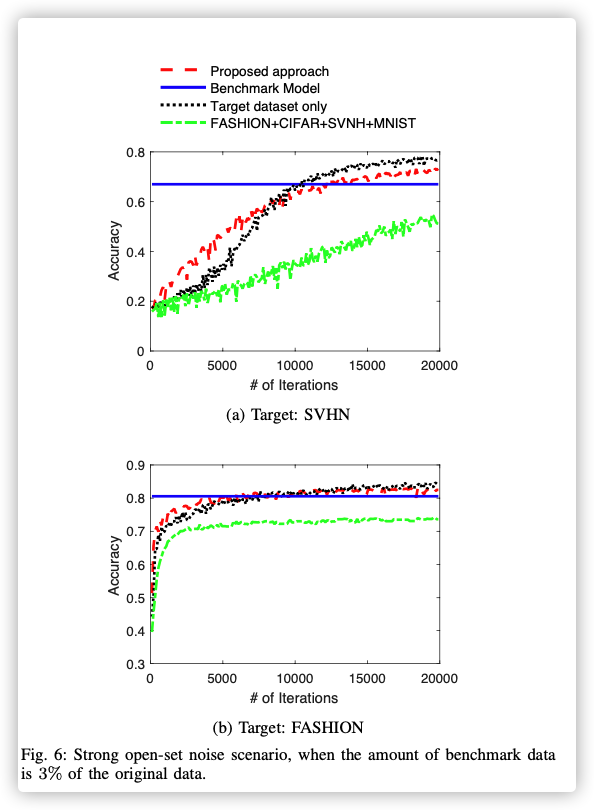
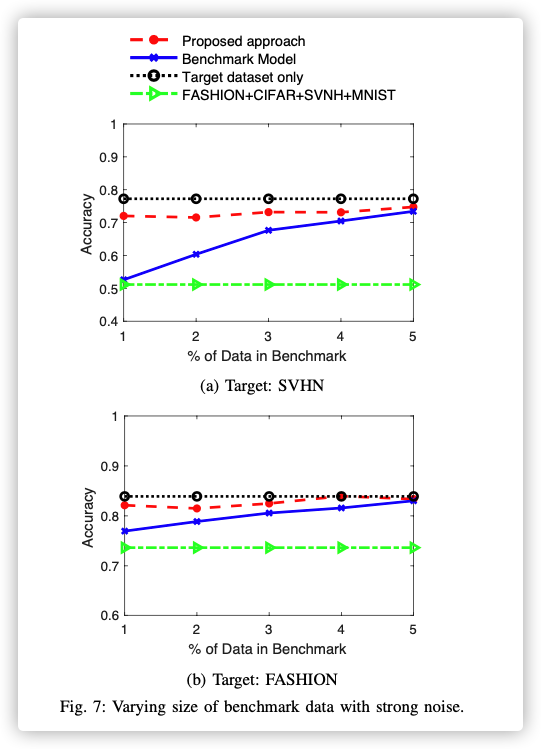
-
Completion Time
个人观点:通篇读下来,没啥障碍难度,这是因为没有严格的数学证明,而是用来大量的 we assume之类的字样。。。