Client Selection for Federated Learning With Non-IID Data in Mobile Edge Computing
0x00 Abstract
A main challenge of FL is that the training data are usually non-Independent, Identically Distributed (non-IID) on the clients, which may bring the biases in the model training and cause possible accuracy degradation. To address this issue, this paper aims to propose a novel FL algorithm to alleviate the accuracy degradation caused by non-IID data at clients. Firstly, we observe that the clients with different degrees of non-IID data present heterogeneous weight divergence with the clients owning IID data. Inspired by this, we utilize weight divergence to recognize the non-IID degrees of clients.
Key Words: Federated Learning,Client Selection
0x01 INTRODUCTION
‘‘Federated learning with non-IID data’’ proposes that the public data could be distributed to clients such that the clients’ data become IID.
The work in ‘‘Hybrid-FL for wireless networks: Cooperative learning mechanism using non-IID data’’ proposes a Hybrid-FL scheme, which allows a few number of clients to upload their data to a FL server.
The work in ‘‘Astraea: Self-balancing federated learning for improving classification accuracy of mobile deep learning applications’’ assumes that the clients are willing to send their data distribution/label information to the server.
However, few work studies how to identify the non-IID degrees of the data at clients.
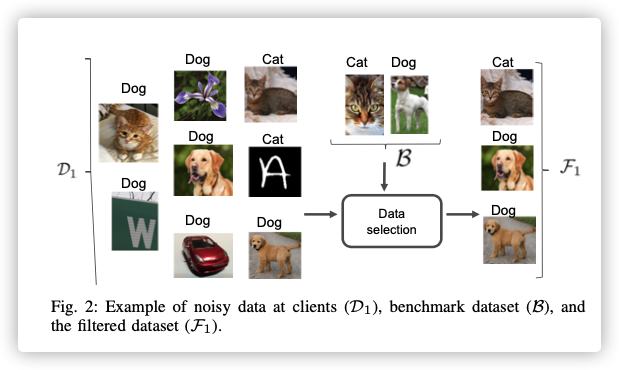
Similar to ‘‘Federated learning with non-IID data’’ , we assume that there exists a limited amount of approximately uniform data, which could be gathered from clients (e.g., 1% of the collection of the data from clients) or public available data.
Main Contribution:
- We define between clients, and observe that larger value of weight divergence indicates higher non-IID degree of data at client.
- Based on weight divergence, we propose an efficient client selection algorithm (CSFedAvg), in which clients with lower non-IID degrees of data will be more often chosen in training.
0x02 PRELIMINARY
There are the following two questions:
How to differentiate the clients according to the degrees of their non-IID data, and choose them in the model training?
If we let the clients with lower degree of non-IID data participate in the training more often than the clients with higher degree of non-IID data, whether the accuracy of FL can be improved or not?
0x03 THE DESIGN OF CSFedAvg
A. OBSERVATION ON WEIGHT DIVERGENCE BETWEEN CLIENT MODELS
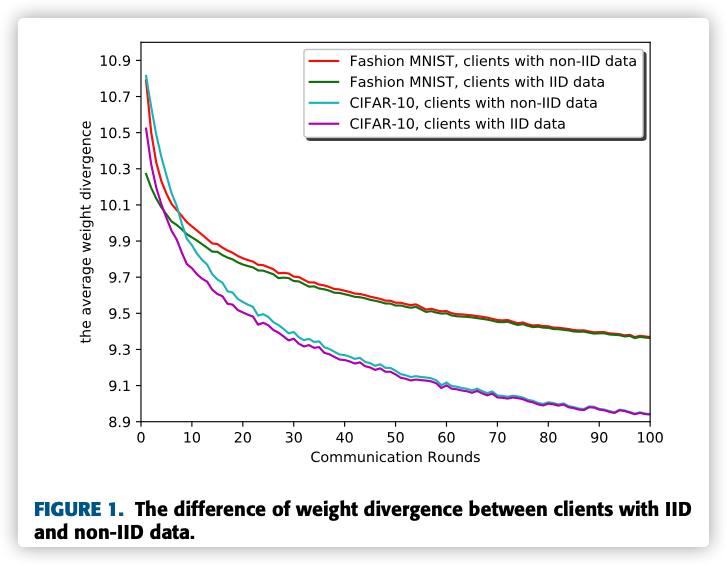
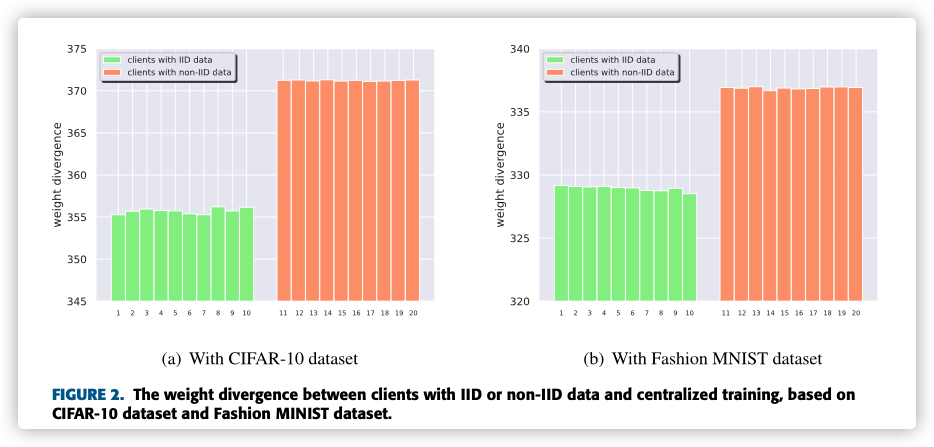
An intuition is that the divergence of models between clients with all IID data should be smaller than one of clients with non-IID data.
本文定义权重差异(WD)如下:
然后做实验观察,这种定义是否合适。
It is observed that the average weight divergence of the clients with non-IID data is always higher than the clients with IID data, which confirms our intuition.
Furthermore, the weight divergence of clients with IID data is very close to each other.
直觉需要验证的,这里的直觉用实践验证了,或许就是启发式吧。。。
本文假设: 服务器端拥有一些辅助的 IID数据集。
B. THE FRAMEWORK OF CSFEDAVG
CSFedAvg的主要核心就是利用自己的辅助数据集,去评估训练节点数据分布是否与该辅助数据集很接近。
因为隐私问题,不能直接访问数据,所以将分布的差异反映到模型上。两个模型差异越小,表示数据分布越接近,在训练的过程中要尽量选择这样节点的模型。
中央服务器会记录 候选节点集 和 最终选择集,候选节点集就是 最终选择集的候选。
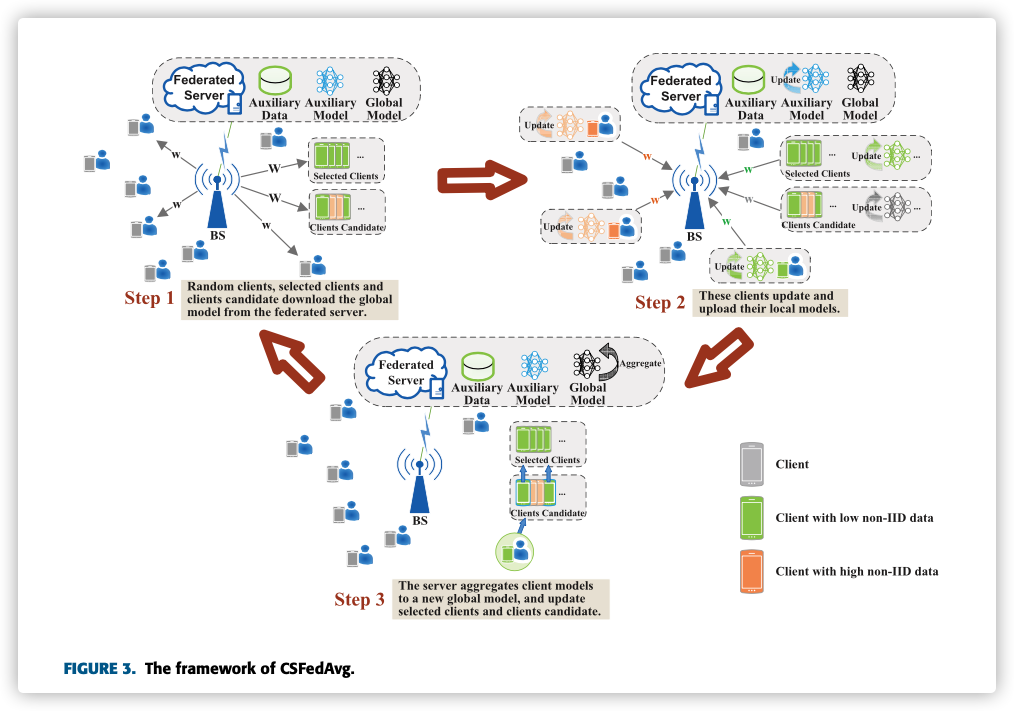
CSFedAvg FL 主要过程如下:
-
Global Model Downloading中央服务器随机选择一些节点构成
随机节点集。该类节点和候选节点集的节点,从中央服务器下载模型。
-
Client Model Update-
上述节点进行本地模型训练。
-
中央服务器用辅助数据集训练进行本地训练。
-
-
Client Set Update and Model Aggregation- 利用中央模型与节点上传模型之间的WD,更新候选节点集和最终选择集。
- 基于
随机节点集和最终选择集进行模型聚合更新 (候选节点集不参与聚合)。
-
重复上述条件,直至到达固定轮数或目标准确值
C. THE ALGORITHM DESIGN OF CSFedAvg
符号解释:
- :随机节点集、候选节点集、最终节点集
- :节点在第轮的模型、中央服务器使用辅助数据训练的模型
- :两个选择比例,超参
CSFedAvg在第轮主要过程:
-
中央服务器随机选择 个节点构成。下载中央模型并训练,中央服务器也用辅助数据集训练
-
上传其本地模型
-
中央服务器计算模型间WD,用表示:
-
根据WD对的模型进行排序(
从小到大):- 如果,从中选择前个加入(退出条件:全部考虑完或)
- 更新为前
- 如果,中央服务器直接进行模型聚合(此处聚合的是以及的模型,详见
算法1)
- 如果,从中选择前个加入(退出条件:全部考虑完或)
-
模型聚合:
-
如果未满,聚合方式如下:
-
如果已满,聚合方式如下:
-
-
直到满足循环结束条件
算法1:

算法2:

这里需要注意的是是一个
只进不出的集合,这里反映了节点的历史贡献。
但
只进不出也需要思考,在模型初期,WD相近就绝对反映出数据分布相近吗?两个比例超参怎么设置才合适?实验也只是进行探索,并无证明,这个超参是否还与辅助数据集大小相关?
这个辅助数据集的分布是直接决定的选取!
如果这个辅助数据集很小?有必要一直伴随着训练吗?会不会过拟合?如果很大,那验证集的准确率是否是因为辅助数据集提高的?
0x04 SIMULATION RESULTS
A. SETUP
-
DataSet:CIFAR-10、Fashion MNISTThese two datasets will be dis- tributed to clients, with each client holding 500 sam- ples of CIFAR-10, and each client holding 600 samples of Fashion MNIST.
-
For both Hybrid I and Hybrid II settings, only a small number of clients, clients are assigned with IID data, while other clients are randomly assigned by images from a few certain limited classes.
这里还需要部分节点的数据是IID的。
-
CNNSpecifically, we set four 3 × 3 convolution layers (32, 32, 64, 64 channels, each of which was activated by ReLU and batch normalized, and every two of which were followed by 2 × 2 max pool- ing), two fully connected layers (384 and 192 units withReLU activation), and a final output layer with 10 units for training both CIFAR-10 and Fashion MNIST datasets.
-
P=0.1,Mini-batch SGD -
Baseline:FedAvg,FedProx
B. PERFORMANCE COMPARISON ON TRAINING ACCURACY
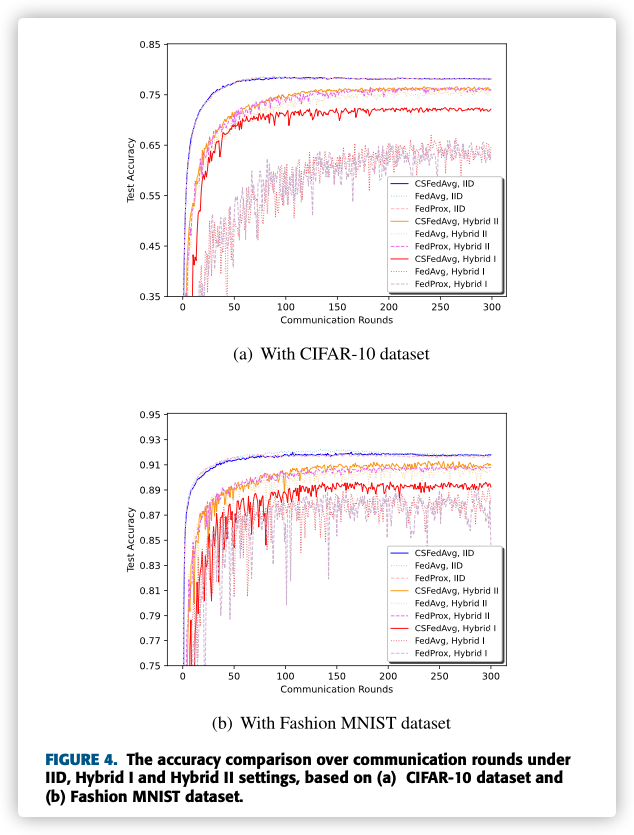
There are two reasons why CSFedAvg can mitigate more accuracy loss on Hybrid I setting.
Firstly, clients with higher degree of non-IID data will lead to larger weight divergence, when the number of clients with IID data and non-IID data is constant.
Secondly, clients with higher degree of non-IID data can accelerate the degradation of the global model performance.
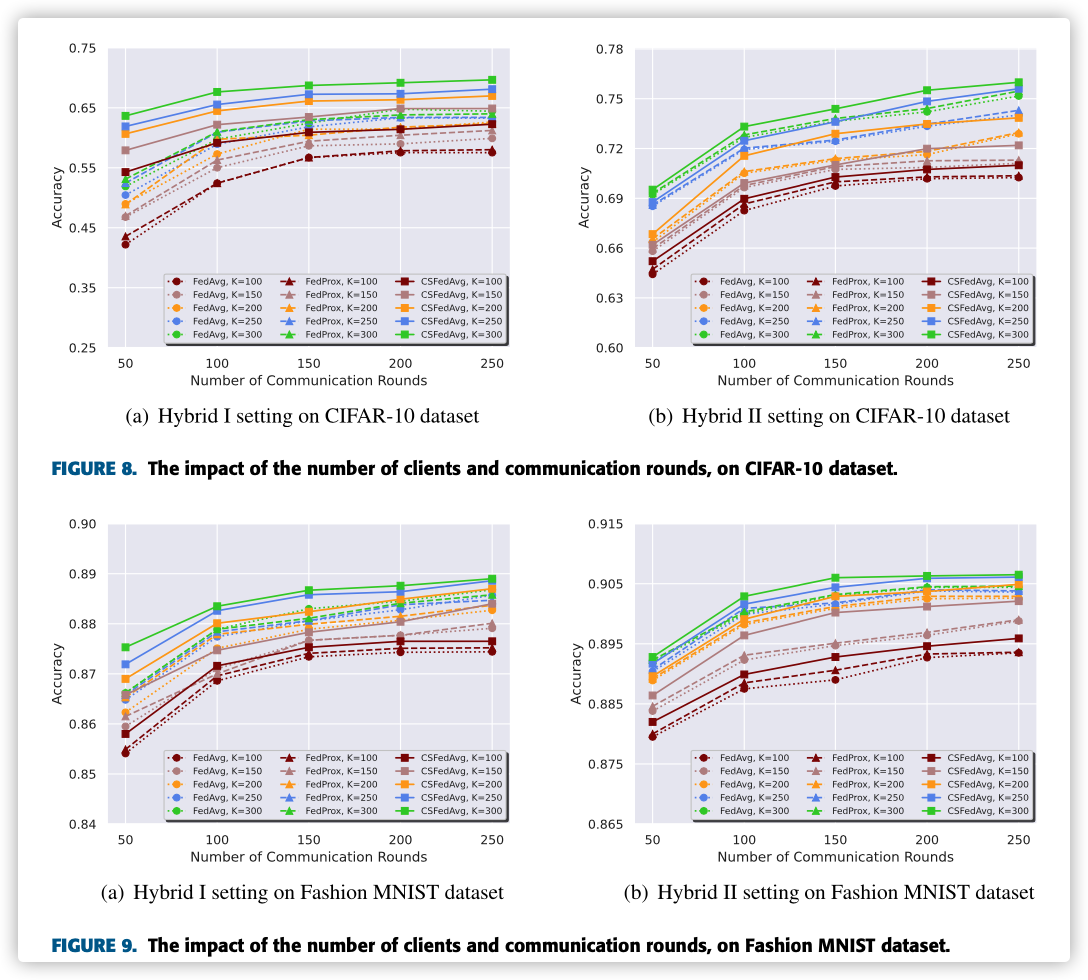
C. PERFORMANCE COMPARISON ON THE NUMBER OF COMMUNICATION ROUNDS
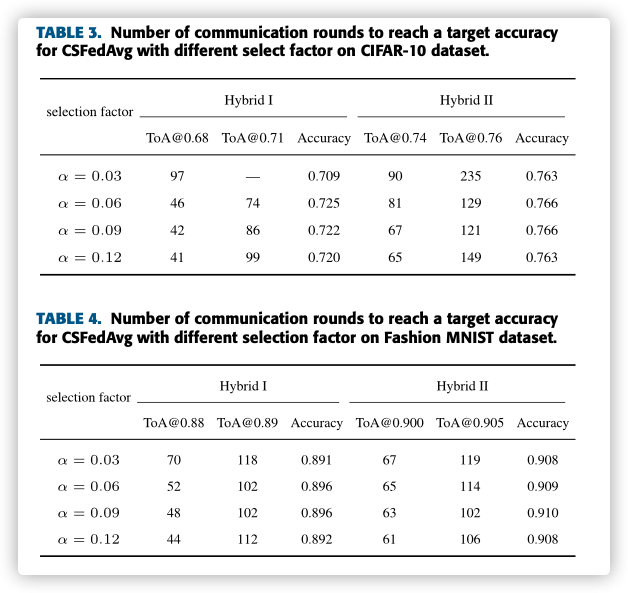
We record the Time of Arrival at a desired accuracy, denoted by ToA@x, where x denotes the target accuracy. Similarly, we measure the accu- racy of each algorithm after running 300 rounds, denoted by in the table.
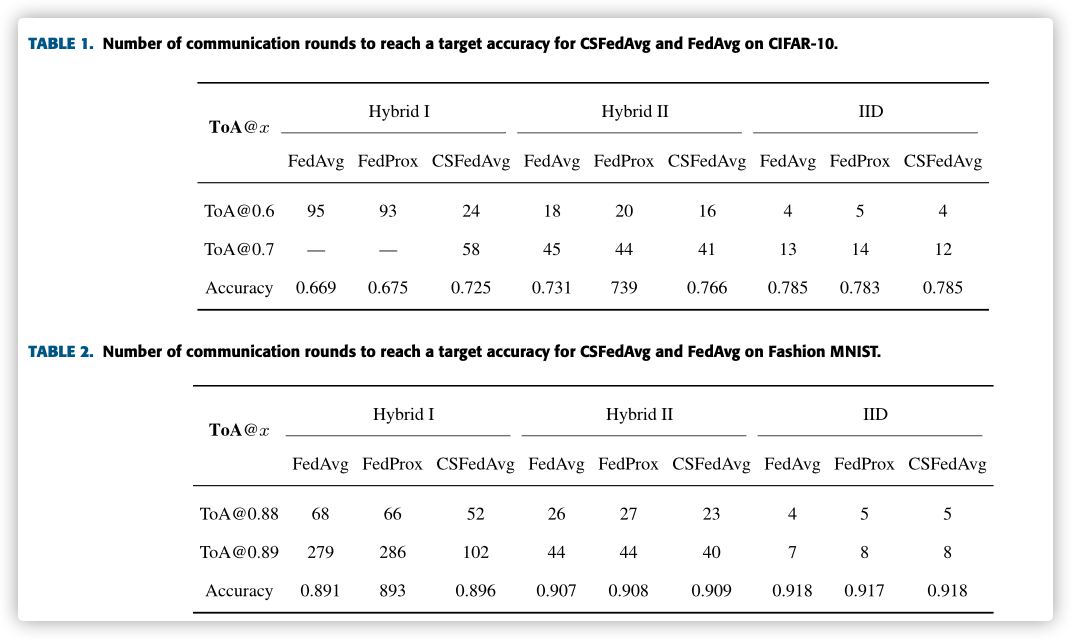
emmm, 739?893?没检查出来?
D. THE IMPACT OF SELECTION FACTOR ON ACCURACY AND COMMUNICATION ROUNDS
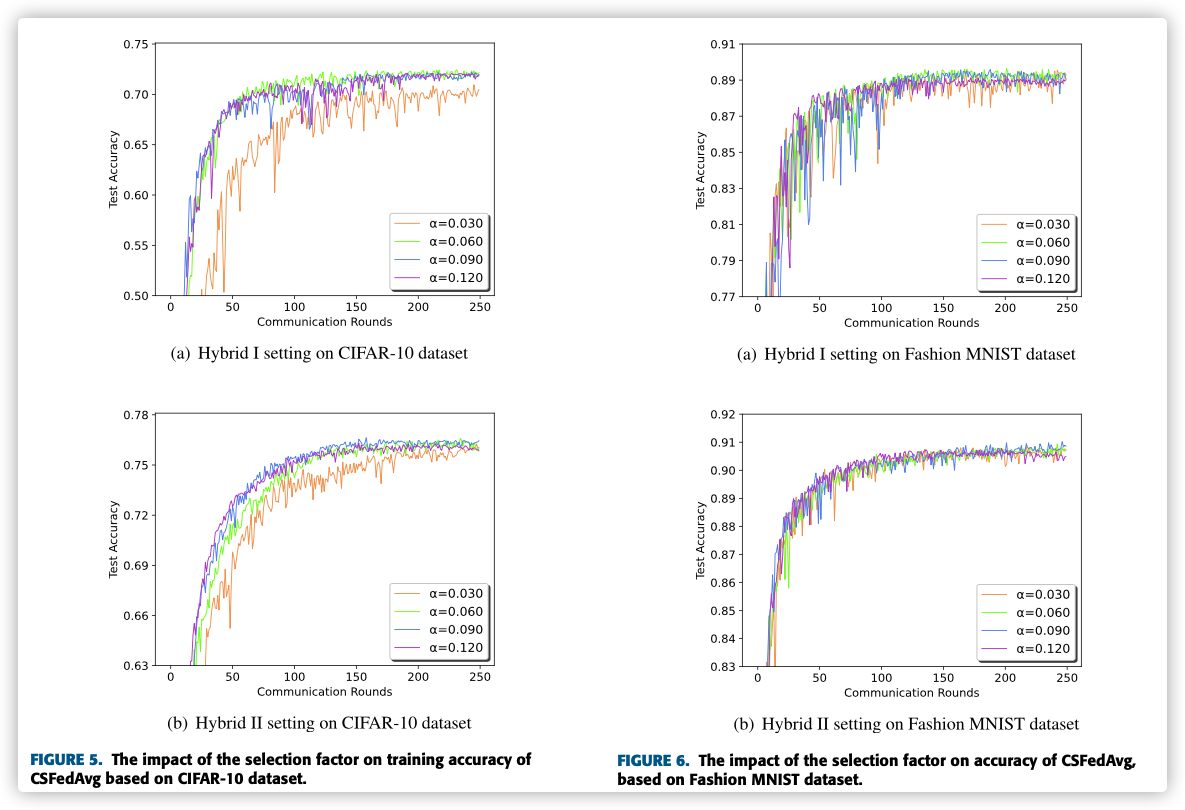
we record the number of communication rounds required to reach a target accuracy based on both CIFAR-10 and Fashion MNIST datasets.
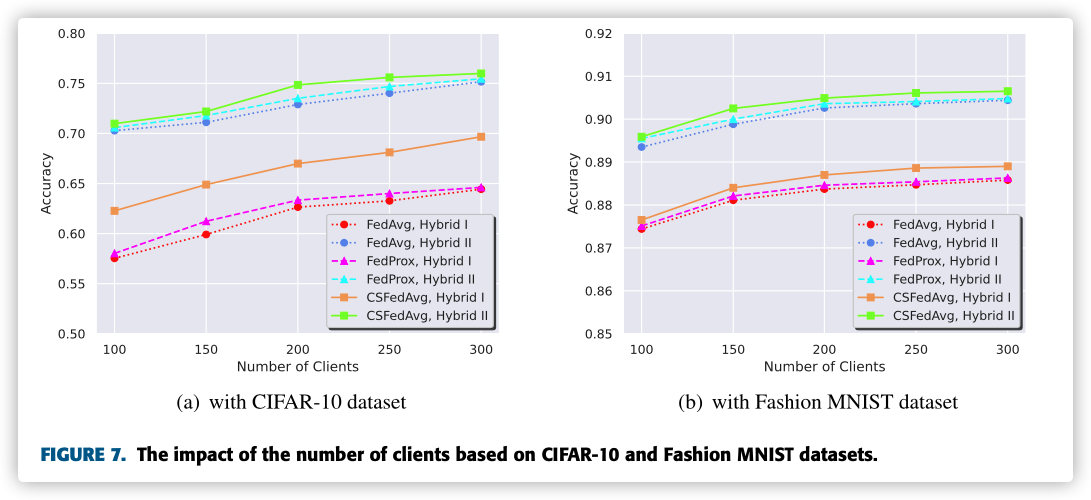
E. THE IMPACT OF THE NUMBER OF CLIENTS
F. THE IMPACT OF GLOBAL IMBALANCED DISTRIBUTION
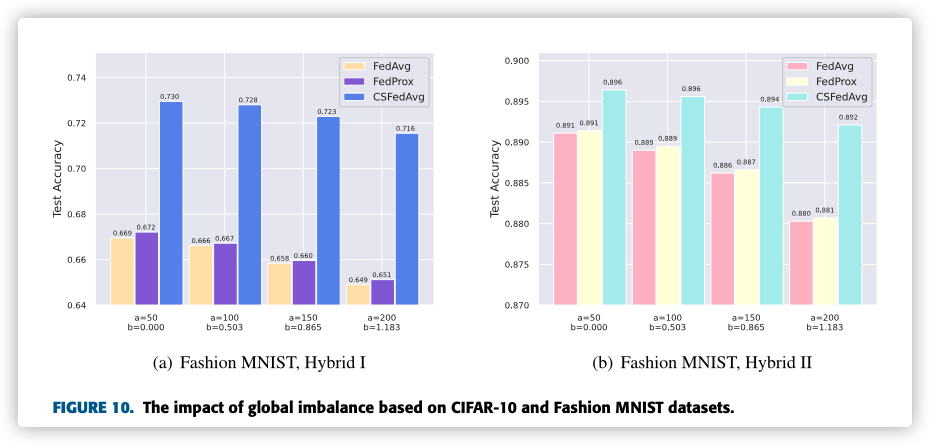
工作量挺大的。。。最后柱状图不是从0开始,故意给人视觉错觉!(小细节!)