Bandit-based Communication-Efficient Client Selection Strategies for Federated Learning
0x00 Abstract
While most prior works assume uniform and unbiased client selection, recent work on biased client selection has shown that selecting clients with higher local losses can improve error convergence speed.
In this paper, we present a bandit-based communication-efficient client selection strategy UCB-CS that achieves faster convergence with lower communication overhead.
Key Words: Federated Learning,Client Selection,Multi-armed bandits
0x01 INTRODUCTION
Due to the inherent data heterogeneity across clients, judicious use of bias in client selection presents an untapped opportunity to improve error convergence.
However the client selection strategies proposed in previous works either require the server to additionally communicate with clients to retrieve the accurate local loss values or use stale loss values received from selected clients from previous communication rounds. Communication is expensive in FL, and furthermore, we show that using stale loss values can lead to slower error convergence or even divergence.
In this paper, we propose a bandit-based client selection strategy UCB-CS that is communication-efficient and use the observed clients’ local loss values more appropriately instead of using stale values.
To the best of our knowledge, there has been no work that proposes or evaluates biased client selection strategies in the context of fairness.
0x02 PROBLEM FORMULATION
A. Federated Learning with Partial Device Participation
A central aggregating server optimizes the model parameter by selecting a subset of clients for some fraction in each communication round (partial-device participation).
The set of active clients at iteration is denoted by . Since active clients performs steps of local update, the active set also remains constant for every iterations.
B. Biased Client Selection for Faster Convergence
It has been noted in [1], [4] that selecting clients with higher local loss at each communication round leads to faster convergence but incurs an error floor.
Under the scheme, the central server with clients obtains their local loss for the current global model . A drawback of scheme is that it requires additional communication, as the central server is required to poll clients before selecting clients for the next communication round.
To reduce this additional communication, it is desirable to have a proxy for the local loss of each client available at the center. Motivated by this, [1] proposes the scheme, where the local loss is approximated by the local loss of the client when it was last selected in the client selection procedure. However, this approximation can be misleading at times as the client loss evaluation can be noisy and stale. Due to these reasons, it was observed that in certain cases the scheme does not have desirable convergence.
- [1] Y. J. Cho, J. Wang, and G. Joshi, “Client selection in federated learning: Convergence analysis and power-of-choice selection strategies,” vol. abs/2010.01243, 2020. [Online].
- [4] J. Goetz, K. Malik, D. Bui, S. Moon, H. Liu, and A. Kumar, “Active federated learning,” ArXiv, 2019.
C. Fairness in Client Selection
According to (1), clients with larger will intuitively yield lower local loss performance, and vice versa.
However, if clients with small perform significantly worse than the other clients, this can be unfair.
We show that client fairness can be improved by incorporating the estimated local loss values and client’s selected frequency to the client selection scheme.
We measure fairness by the Jain’s index , where 1 is when all clients have the same performance.
Q:
Why is it unfair using ?
0x03 CLIENT SELECTION WITH DISCOUNTED UCB
In order to achieve faster convergence with low error floor, it is important to select clients with larger local loss (i.e., exploitation) as that leads to faster convergence. It is also important to ensure diversity (i.e., exploration) in selection to achieve a lower error floor.
知识补充:Multi-armed bandits
多臂老虎机问题:一个赌徒,要去摇老虎机,走进赌场一看,一排老虎机,外表一模一样,但是每个老虎机吐钱的概率可不一样,他不知道每个老虎机吐钱的概率分布是什么,那么每次该选择哪个老虎机可以做到最大化收益呢?
**核心:**根据估值选择最优的动作,与强化学习如出一辙。
最直观的是使用采样平均获取参考依据,分别表示收益均值、回报、动作:
随着实验次数的增加,就会越接近真实值。
exploitation(开发):一直选择产出最大的老虎机,这个产出就是根据历史经验获取的。
exploration(探索):选择其他的老虎机,基于历史经验可能会进入局部最优。
例:比如对10个老虎机,每个只拉一次,会有可能有个老虎机一般产出不行,但是就在你采样的这次,产出爆棚,你就会以为它就是最棒的,后期会一直选择它,这样就会错过全局最优的老虎机!
贪心改进:
如果一直不探索,就是贪心算法。对其稍微进行改进就是 算法,每次选择会有的概率选择探索。
置信度上界(UCB):
UCB估计其实就是在某个置信度下,取置信区间的上界作为估计.
其中表示从开始到选择动作的次数,表示置信水平。
特别的,时,就是最优动作。
随着实验次数的增加,使得估值更接近真实值。
通过增加出现次数少的action的选择概率来增强Exploration
扩展:
UCB很难转化到强化学习中
本文计算第个设备在第次通信中的UCB指标如下:
-
exploitation: ,explpration: -
表示对历史参考的重要性:
- ,均等地对待历史事件,没有遗忘性
- ,完全不考虑历史事件
-
,设备到通讯轮数被采样次数
-
-
和置信度一样,表示对待未被采用节点的重视程度
详细算法如下:

0x04 EXPERIMENT RESULTS
DNNFMNISTNon-IIDPyTorchNVIDIA TitanX GPU
实验结果:
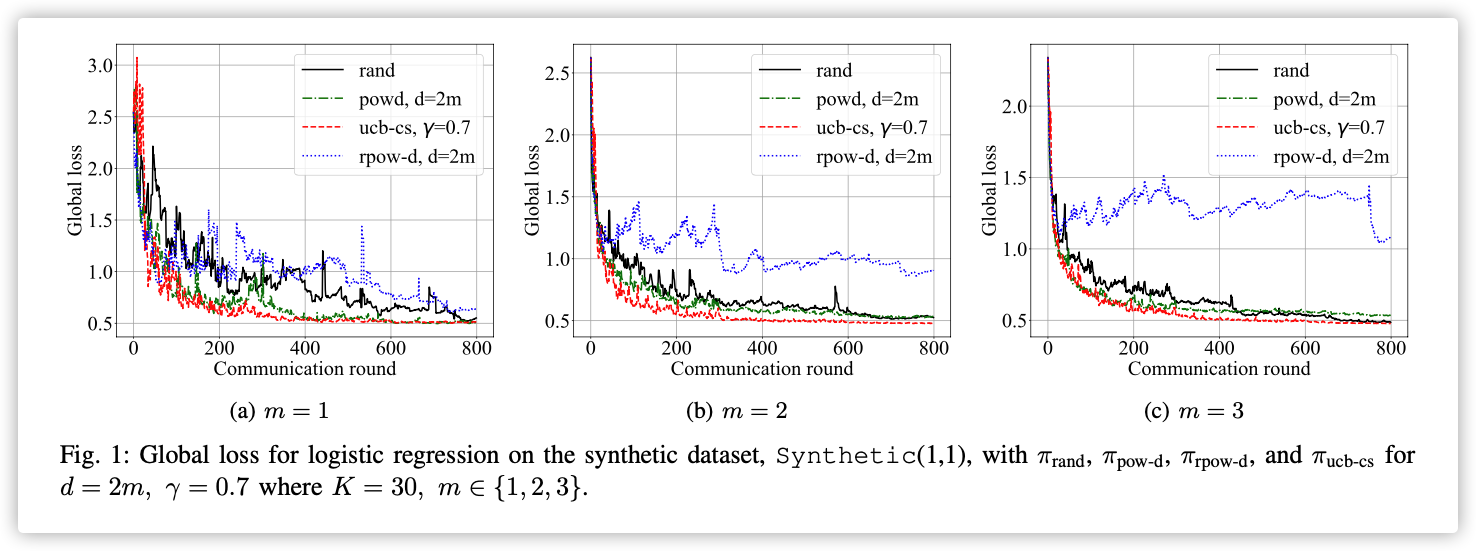
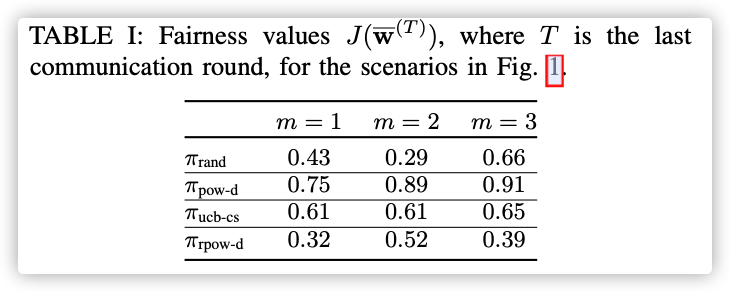
Hence we show that is efficient in the three important factors in FL: loss performance, fairness, and communication-efficiency.
这个Jain公平指标越接近1越好?!
虽然的公平值比低,但是通信开销和最终损失低啊…
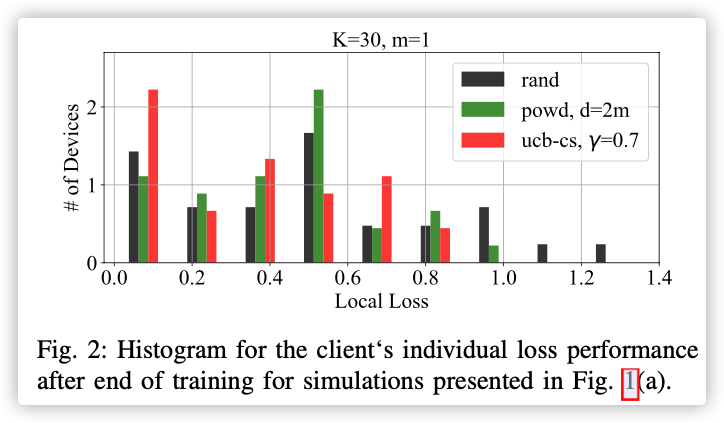
30个设备每次选一个聚合,最后观察每个节点上的损失。
从图中看出策略的设备损失偏低。
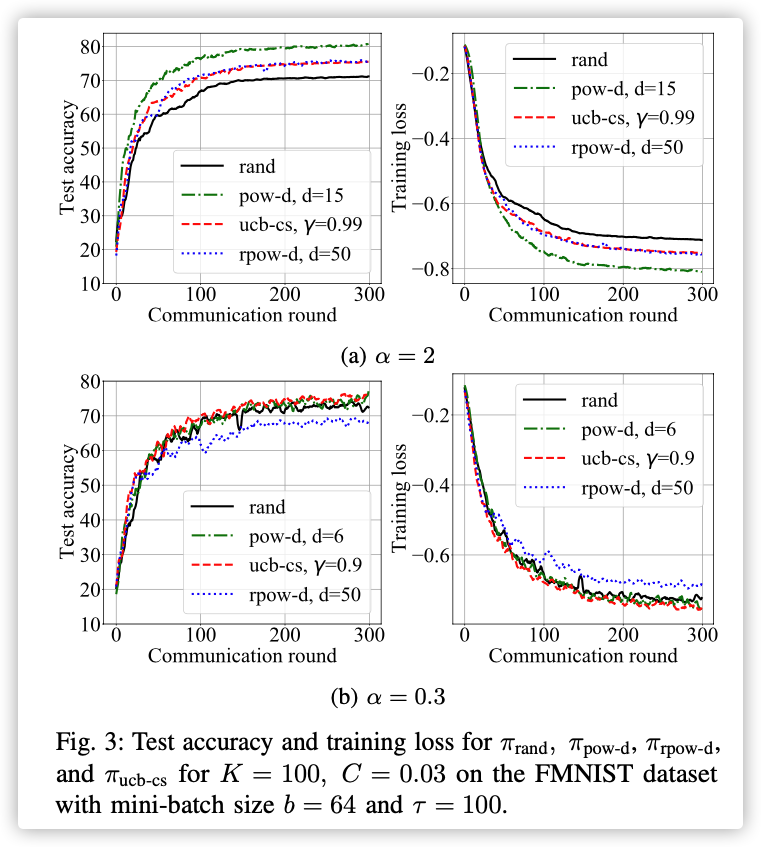
表示设备之间的差异性,越小差异越大。
这几个图看的一脸懵逼…
参考
- 多臂赌博机
- 《统计学习方法》
- Hoeffding‘s Inequality