Client Selection for Federated Learning with Heterogeneous Resources in Mobile Edge
0x00 Abstract
The FL protocol iteratively asks random clients to download a trainable model from a server, update it with own data, and upload the updated model to the server, while asking the server to aggregate multiple client updates to further improve the model. While clients in this protocol are free from disclosing own private data, the overall training process can become inefficient when some clients are with limited computational resources (i.e., requiring longer update time) or under poor wireless channel conditions (longer upload time).
Our new FL protocol, which we refer to as FedCS, mitigates this problem and performs FL efficiently while actively managing clients based on their resource conditions. Specifically, FedCS solves a client selection problem with resource constraints, which allows the server to aggregate as many client updates as possible and to accelerate performance improvement in ML models.
Key Words: Federated Learning, Client Selection,Greedy Algorithm
0x01 INTRODUCTION
In particular, we consider the problem of running FL in a cellular network used by heterogeneous mobile devices with different data resources, computational capabilities, and wireless channel conditions.
Our main contribution is a new protocol referred to as FedCS, which can run FL efficiently while an operator of MEC frameworks actively manages the resources of heterogeneous clients. Specifically, FedCS sets a certain deadline for clients to download, update, and upload ML models in the FL protocol.
This is technically formulated by a client- selection problem that determines which clients participate in the training process and when each client has to complete the process while considering the computation and communication resource constraints imposed by the client, which we can solve in a greedy fashion.
0x02 FEDERATED LEARNING
A. Federated Learning

The only technical requirement is that each client must have a certain level of computational resources because Update and Upload consists of multiple iterations of the forward propagation and backpropagation of the model
B. Heterogeneous Client Problem in FL
Protocol 1 can experience major problems while training ML models in a practical cellular network, which are mainly due to the lack of consideration of the heterogeneous data sizes, computational capacities, and channel conditions of each client.
All such problems about heterogeneous client resources will become bottlenecks in the FL training process; the server can complete the Aggregation step only after it receives all client updates. One may set a deadline for random clients to complete the Update and Upload step and ignore any update submitted after the deadline. However, this straight-forward approach will lead to the inefficient use of network bandwidths and waste the resources of delayed clients.
0x03 FEDCS: FEDERATED LEARNING WITH CLIENT SELECTION
A. Assumptions
- 在无线网络稳定不堵塞的情况,例如夜间或清晨
- 终端的网络资源块(RBs:带宽资源最小单位)是受限的,并且由MEC管理
- 多个节点同时传输模型,每个节点的吞吐量会降低
- 通信的编码模式是预先设定的,丢包率可以忽略
每个节点的信道状况和吞吐量是固定的!
B. FedCS Protocol

与传统的联邦协议不同的部分就是节点选择部分,此协议将节点选择分为两部分:
Resource Request:被随机选中的节点需要给MEC上传自己的资源信息,例如网络状况、算力、任务相关数据集大小Client Selection:MEC根据获得的资源信息,评估每个节点处理Distribution和Scheduled Update and Upload所需要耗费的时间,并以此决定选择哪些节点加入训练
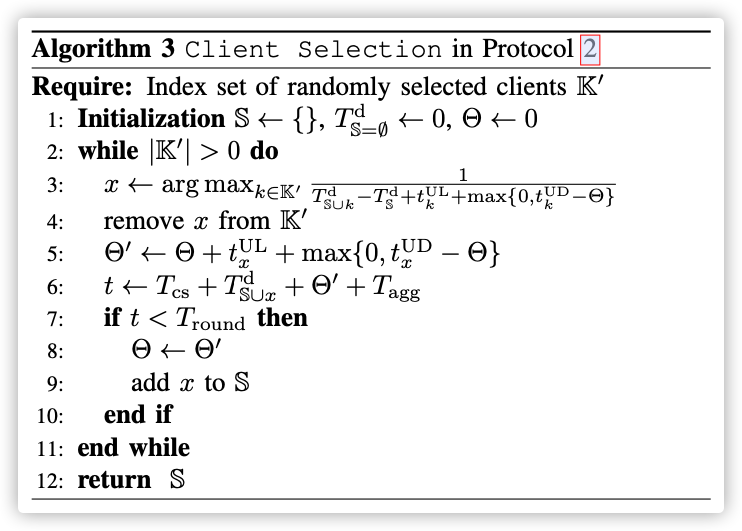
C. Algorithm for Client Selection Step
本段是本论文比较核心的地方,用贪心算法,对节点上传模型进行排序,目的是在规定的时间内尽量多的节点上传。
Our goal in the Client Selection step is to allow the server to aggregate as many client updates as possible within a specified deadline.
在MEC选择节点的同时,也会给选中的节点安排可用网络资源块,以防网络拥堵的情况发生!本文假设节点完成模型的更新后,会依次上传模型(One by One)!
符号说明:
:表示个节点的索引集合
:表示在 Resource Request环节被选中节点的索引,通常个数为
:表示被选中节点的索引序列,这些索引是参加聚合过程的索引,因此.
这个序列怎么排就是本文需要优化的问题!
:分别表示每轮时间限制,总时间限制,Client Selection、Distribution 阶段耗费时间。
:表示节点更新模型、上传模型的时间。
Now, the objective of Client Selection, namely accepting as many client updates as possible, can be achieved by maximizing the number of selected clients, i.e., . To describe the constraint, we define the estimated elapsed time from the beginning of the Scheduled Update and Upload step until the -th client completes the update and upload procedures.
为了更好的刻画模型,引入时间序列:
前文提到模型的上传是一个接一个上传的,也就是说在节点之前的设备上传模型的时间,也是节点可以利用来训练模型的时间。这就是整个算法的贪心使用之处(与贪心算法中的排课模型是相同的:在规定的时间内,排上尽量多课程,当时的贪心策略是优先选择结束时间早的课程)
因此当前模型如下:
Optimization strategies:
Selection of :
在总训练时间规定的情况,本地训练轮数与总聚合轮数的 trade-off
0x04 PERFORMANCE EVALUATION
A. Simulated Environment
We simulated a MEC environment implemented on the cellular network of an urban microcell consisting of an edge server, a BS, and K = 1000 clients, on a single workstation with GPUs. The BS and server were co-located at the center of the cell with a radius of 2 km, and the clients were uniformly distributed in the cell.
- 考虑信号强度
- 为终端算力引入高斯分布,更加仿真
- 考虑中央服务器的高性能,将
B. Experimental Setup of ML Tasks
- DataSet:
CIFAR-10和Fashion MNIST - 每个设备拥有数据量从
100~1000不等 - 分为
Non-IID和IID实验 - 节点选择:
100/1000
C. Global Models and Their Updates
-
卷积网络:
Our model consisted of six 3 × 3 convolution layers (32, 32, 64, 64, 128, 128 channels, each of which was activated by ReLU and batch normalized, and every two of which were followed by 2 × 2 max pooling) followed by three fully-connected layers (382 and 192 units with ReLU activation and another 10 units activated by soft-max).
CIFAR-10:4.6 million 模型参数Fashion MNIST: 3.6 million 模型参数 -
50 for mini-batch size, 5 for the number of epochs in each round, 0.25 for the initial learning rate of stochastic gradient descent updates, and 0.99 for learning rate decay
-
We determined the mean capability of each client randomly from a range of 10 to 100, which are used the value for
Client Selection. -
As a result, each update time, , used in Client Selection varied from 5 to 500 k seconds averagely.
-
we empirically set to 3 minutes and to 400 minutes.
D. Evaluation Details
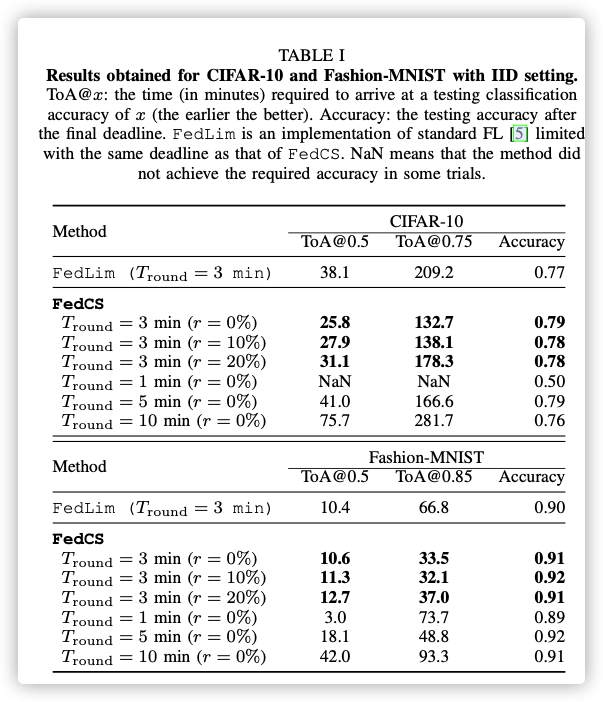
E. Results
IID setting:
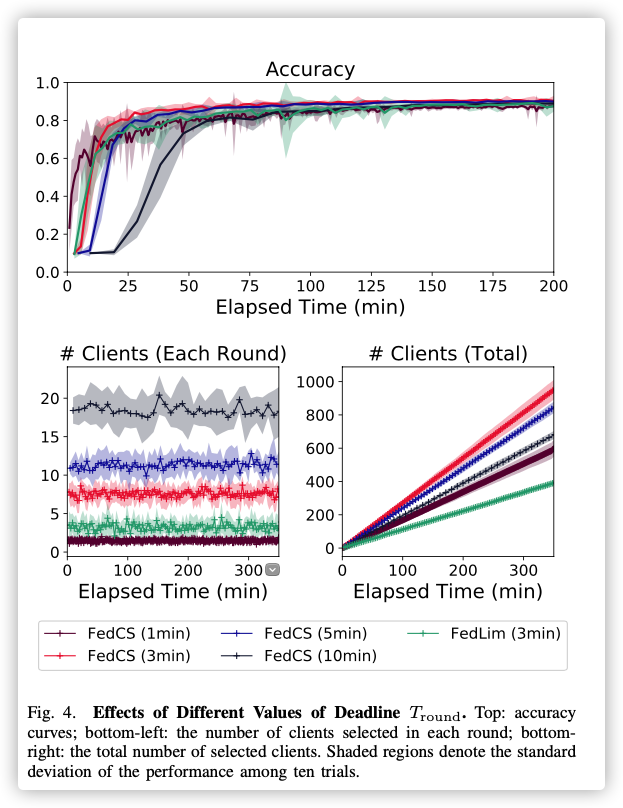
Nevertheless, our selection of model architectures was suf- ficient to show how our new protocol allowed for efficient training under resource-constrained settings and was not for achieving the best accuracies.
- 算力添加高斯不会对
FedCS算法造成影响- 太大、太小都不行!
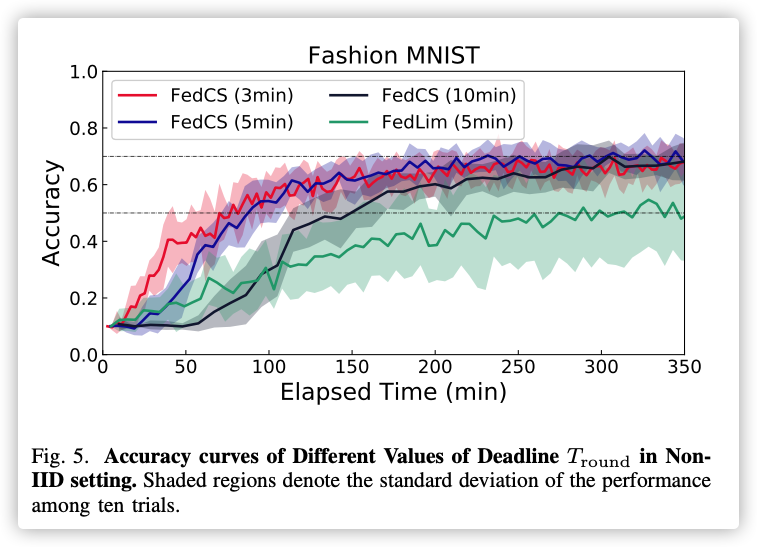
Non-IID setting:
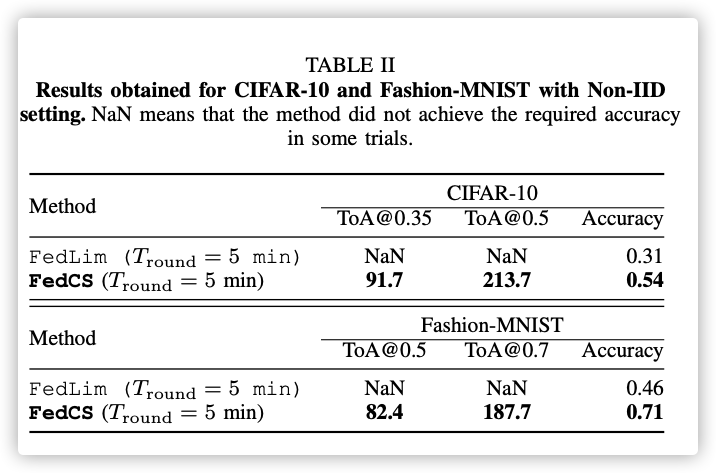
普通算法没有达到性能标准…