神经网络--tensorflow
记录一下coding中遇到的问题
四月是你的谎言
杂味
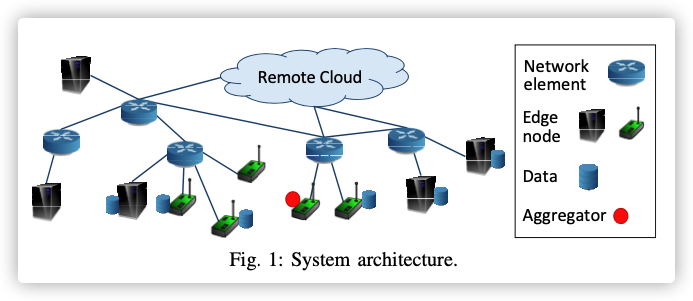
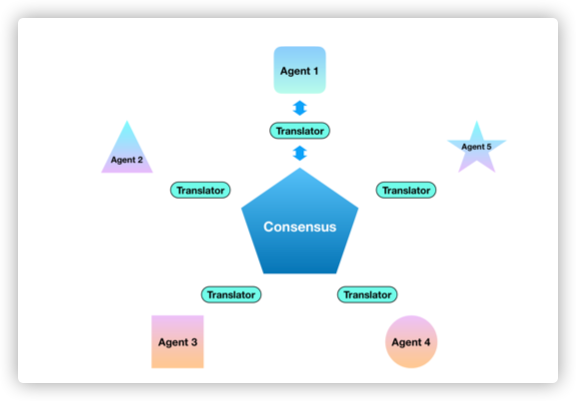
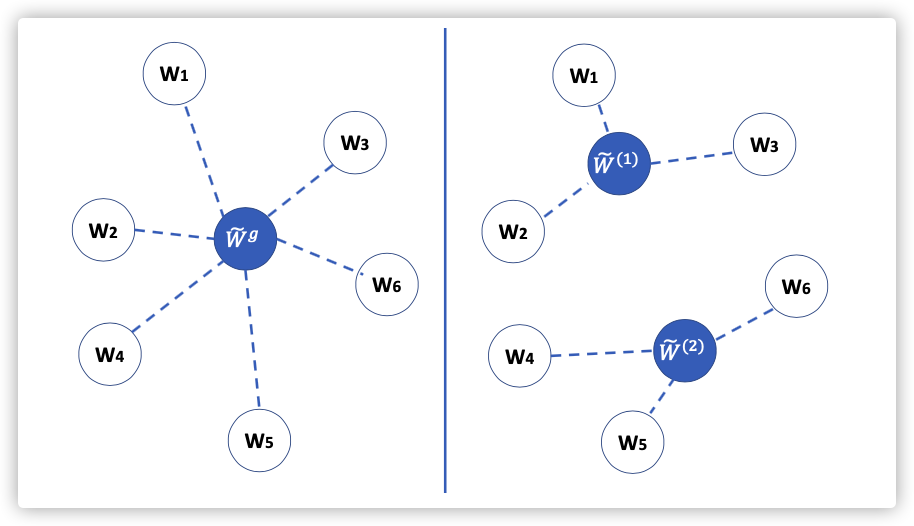
Multi-Center Federated Learning
多个训练模型同时进行
核方法
核方法
0x01 为什么需要核函数
问题1:
SVM显然是线性分类器,但数据如果根本就线性不可分怎么办?
解决方案1:
数据在原始空间(称为输入空间)线性不可分,但是映射到高维空间(称为特征空间)后很可能就线性可分了。
问题2:
映射到高维空间同时带来一个问题:在高维空间上求解一个带约束的优化问题显然比在低维空间上计算量要大得多,这就是所谓的“维数灾难”。
解决方案2:
于是就引入了“核函数”,核函数的价值在于它虽然也是讲特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就是说避免了直接在高维空间中的复杂计算
例如图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
0x02 什么是核函数
引入:
从上图我们可以看出一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
a1X1+a2X12+ ...
密码学基础题
Problem 1
According to the encryption algorithm,we can get the ciphertext of M3M_3M3 as follow:
C1=CBC−MCk(0n⊕M1)=M2C3=CBC−MCk(C1⊕0n)=CBC−MCk(M2)\begin{aligned}
\begin{array}{l}
C_1=CBC-MC_k(0^n\oplus M_1)=M_2\\
C_3=CBC-MC_k(C_1\oplus0^n)=CBC-MC_k(M_2)
\end{array}
\end{aligned}
C1=CBC−MCk(0n⊕M1)=M2C3=CBC−MCk(C1⊕0n)=CBC−MCk(M2)
It cannot play a role in increasing the difficulty of calculation because M3M_3M3 is padded using 0n0^n0n.
Problem 2
a.
According to the question,we ge ...
Federated Learning with Non-IID Data
好久没看论文了,菜是原罪。。。
下载链接
0x00 Abstract
本文专注于FL中Non-IID的统计困难问题。
用训练节点种类分布的Earth mover’s distance(EMD)量化权重差异度,以此来说明准确下降的问题。
提出了一种数据分享的策略:中央云端共享数据集到各个训练节点!
KEY WORDS:Non-IID,Weight Divergence,EMD
0x01 Introduction
IID数据比较容易训练:
The IID sampling of the training data is important to ensure that the stochastic gradient is an unbiased estimate of the full gradient
0x02 FedAvg on Non-IID data
Setup
训练节点:10
数据集:MNIST、CIFAR-10、KWS
数据分布:
IID:each client is randomly assigned a uniform distribution over 1 ...