Multi-Center Federated Learning
0x00 Abstract
Existing federated learning approaches usually adopt a single global model to capture the shared knowledge of all users by aggregating their gradients, regardless of the discrepancy between their data distributions.
Our paper proposes a novel multi-center aggregation mechanism for federated learning, which learns multiple global models from the non-IID user data and simultaneously derives the optimal matching between users and centers.
We formulate the problem as a joint optimization that can be efficiently solved by a stochastic expectation maximization (EM) algorithm.
Key Words: Federated Learning,clustering,multi-center,EM
0x01 Introduction
Early federated learning approaches use only one global model as a single-center to aggregate the information of all users. The stochastic gradient descent (SGD) for single-center aggregation is designed for IID data, and therefore, conflicts with the non-IID setting in federated learning.
Sattler.F proposed an idea of clustered federated learning (FedCluster) that addresses the non-IID issue by dividing the users into multiple clusters. However, the hierarchical clustering in FedCluster is achieved by multiple rounds of bipartite separation, each requiring to run the federated SGD algorithm till convergence.
We formulate the problem of multi-center federated learning as jointly optimizing the clustering of users and the global model for each cluster such that 1) each user’s local model is assigned to its closest global model, and 2) each global model leads to the smallest loss over all the users in the associated cluster.
Main contribution:
- We propose a novel multi-center aggregation approach (Section 4.1) to address the non-IID challenge of federated learning.
- We design an objective function, namely multi-center federated loss (Section 4.2), for user clustering in our problem.
- We propose Federated Stochastic Expectation Maximization (FeSEM) (Section4.3) to solve the optimization of the proposed objective function.
- We present the algorithm (Section 4.4) as an easy-to-implement and strong baseline for federated learning . Its effectiveness is evaluated on benchmark datasets. (Section 5)
0x02 Related Work
To solve the problem caused by non-IID or heterogeneity data in federated setting:
"Clustered federated learning: Model-agnostic distributed multi-task optimization under privacy constraints" proposed clustered federated learning (FedCluster) by integrating federated learning and bi-partitioning-based clustering into an overall framework.
“Robust federated learning in a heterogeneous environment” proposed robust federated learning composed of three steps: 1) learning a local model on each device, 2) clustering model parameters to multiple groups, each being a homogeneous dataset, and 3) running a robust distributed optimization in each cluster.
“Feddane: A federated newton-type method” proposed FedDANE by adapting the DANE to federated setting. In particular, FedDANE is a federated Newton-Type optimization method.
“Federated optimization in heterogeneous networks” proposed FedProx for a generalization and re-parameterization of FedAvg. It adds a proximal term to the objective function of each device’s supervised learning task, and the proximal term is to measure the parameter-based distance between the server and the local model.
“Federated learning with personalization layers” added a personalized layer for each local model, i.e., FedPer, to tackle heterogeneous data.
0x03 Background
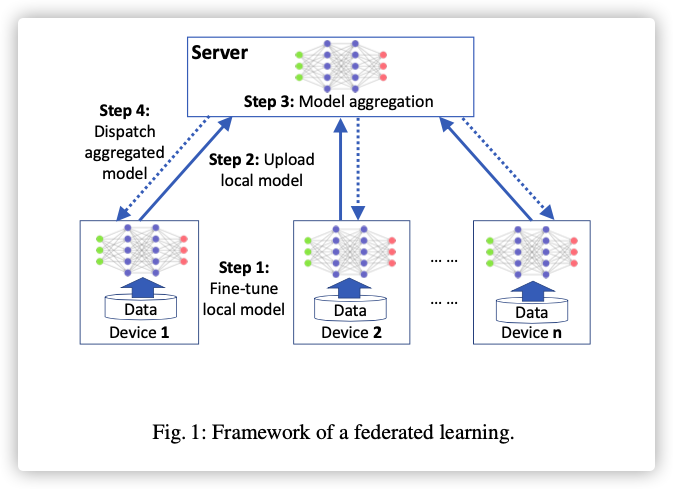
- 在拥有隐私数据的终端进行监督学习,获得模型:
是损失函数,是模型权重。
- 联邦学习考虑到将所有设备的损失函数最小化,根据数据量的多少引入损失的权重,是设备数:
联邦聚合过程改变如下:
0x04 Methodology
1.Multi-center Aggregation
考虑到每个用户的习惯不同,所以本地模型采用的优化方式也是不一样的。
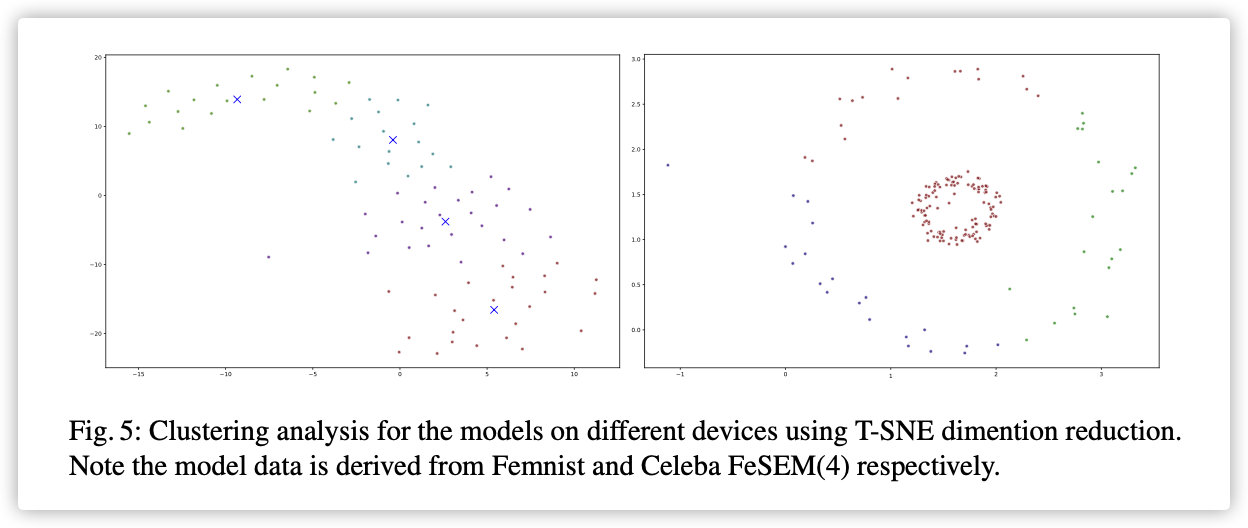
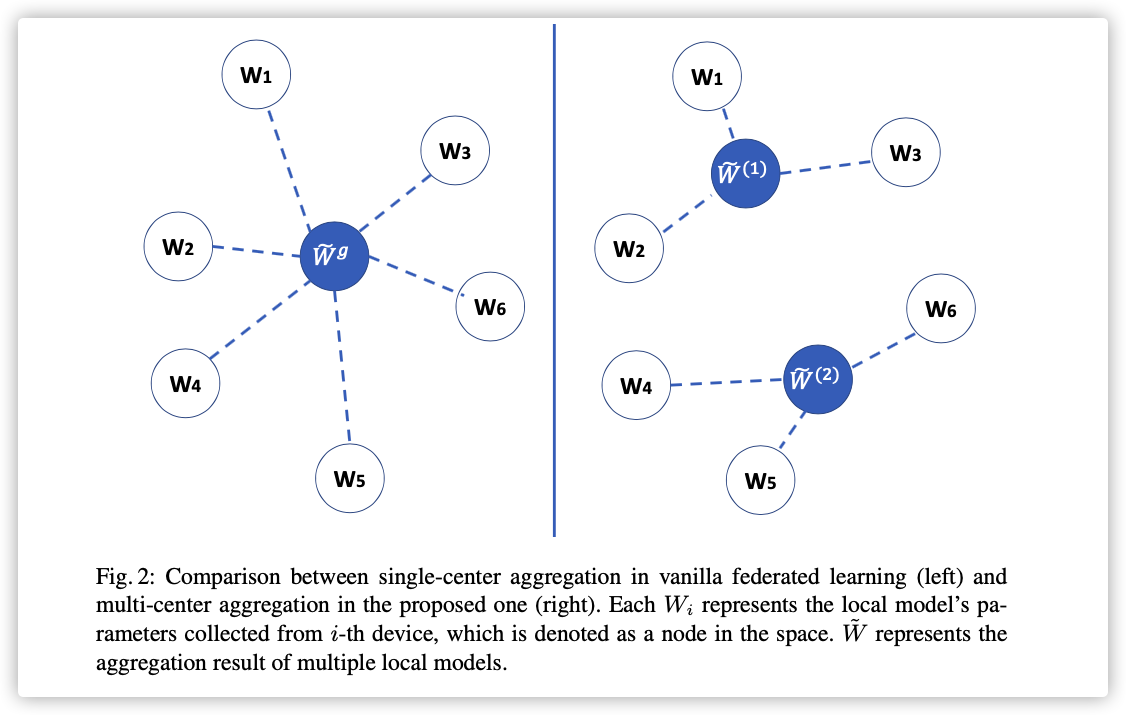
本文将个训练节点根据特定的方式分成组,每个组内做模型聚合。为了描述这个特定的方式,引入了集群间距的概念,如下图:
下图应该是将模型映射到一个二维特征空间,集群间距就是聚合模型到其余模型的距离和。
但是下文并未描述此图的作图根据。
2.Objective Function
为了解决Non-IID问题,本文提出两个联邦损失:
-
distance-based federated loss – a new objective function using a distance between parameters from the global and local models
-
multi-center federated loss – the total distance-based loss to aggregate local models to multiple centers.
Distance-based federated loss(DF-Loss)
基于假设:“较好”的模型初始化更容易收敛到全局最优。
Moreover, considering the limited computation power and insufficient training data on each device, a “good” initialization is vitally important to train a supervised learning model on the device.
这个图的作图依据也没说明…就算给出代码,也是概率复现???
用代替原始损失函数的准确性:
“较好”初始模型越靠近→越容易收敛到→传统损失函数值会降低。
新的目标函数如下(此处未引入权重):
此处的是测量两个模型之间的差距,有多种选择,本文选择了范数:
Multi-center DF-Loss
Furthermore, according to the non-IID assumption, the datasets in different devices can be grouped into multiple clusters where the on-device datasets in the same cluster are likely to be generated from one distribution.
定义集群间距如下(所有集群的所有距离和):
此处指明节点是否属于集群,是集群聚合模型。
3.OPtimization Method
使用EM算法优化,因为是随机初始化,所以使用 Stochastic Expectation Maximization (SEM),步骤如下:
E-step– updating cluster assignment with fixedM-step– updating cluster centers- updating local models by providing new initialization .

E-Step:
M-Step:
updating the local models:the global model’s parameters are sent to each device in cluster to update its local model, and then we can fine-tune the local model’s parameters using a supervised learning algorithm on its own private training data.
4. Algorithm
In particular, in the third step for updating the local model, we need to fine-tune the local model by implementing Algorithm 2.

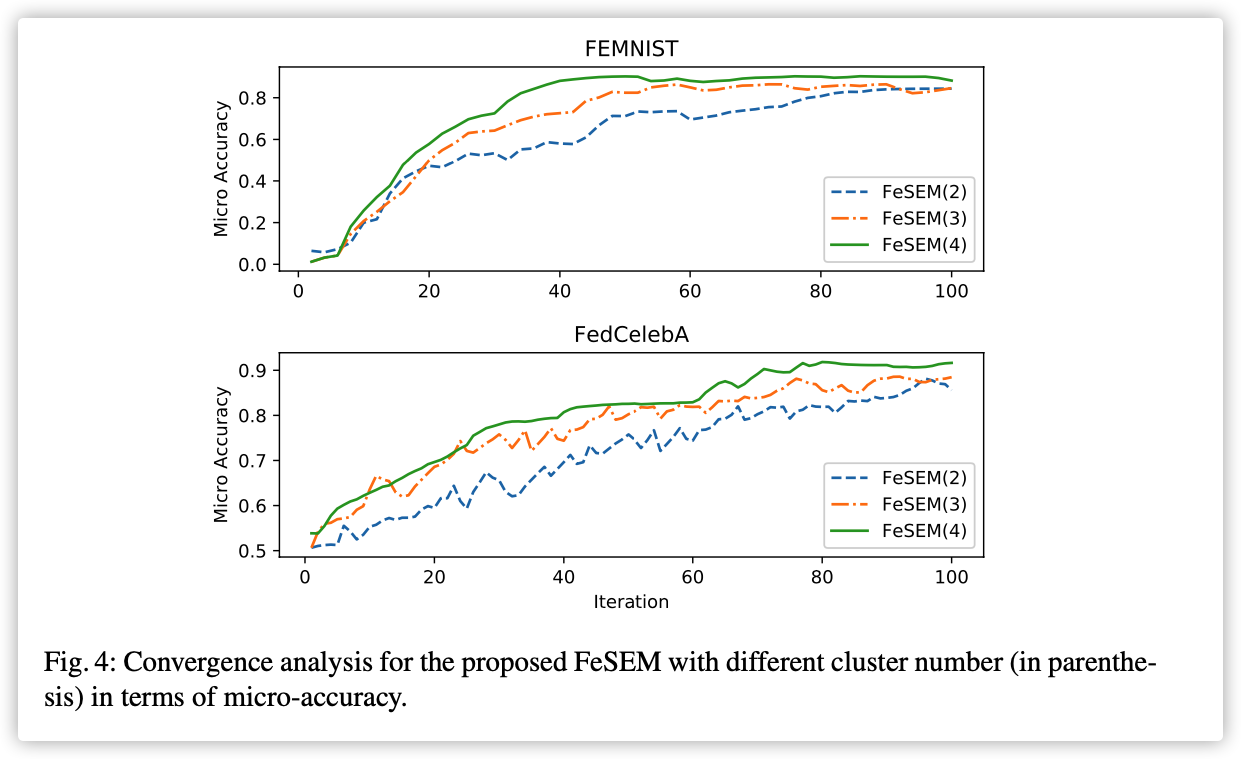
0x05 Experiments