Game of Gradients: Mitigating Irrelevant clients in Federated Learning

AAAI Conference on Artificial Intelligence
0x00 Abstract
Though FL paradigm has received significant interest recently from the research community, the problem of selecting the relevant clients w.r.t. the central server’s learning objective is under-explored. We refer to these problems as Federated Relevant Client Selection (FRCS). Because the server doesn’t have explicit control over the nature of data possessed by each client, the problem of selecting relevant clients is significantly complex in FL settings.
The problems of FRCS need to be resolved:
- selecting clients with relevant data
- detecting clients that possess data relevant to a particular target label
- rectifying corrupted data samples of individual clients.
We follow a principled approach to address the above FRCS problems and develop a new federated learning method using the Shapley value concept from cooperative game theory. Towards this end, we propose a cooperative game involving the gradients shared by the clients. Using this game, we compute Shapley values of clients and then present Shapley value based Federated Averaging (S-FedAvg) algorithm that empowers the server to select relevant clients with high probability.
Key Words:Relevant data,Shapley value,Federated Learning
0x01 Introduction
FL setting assumes a syn- chronous update of the central model and the following steps proceed in each round of the learning process (McMahan et al. 2017).
Note that only a fraction of clients is selected in each round as adding more clients would lead to diminishing returns beyond a certain point.
Though initially the emphasis was on mobile- centric FL applications involving thousands of clients, recently there is significant interest in enterprise driven FL applications that involve only a few tens of clients.
Motivation:
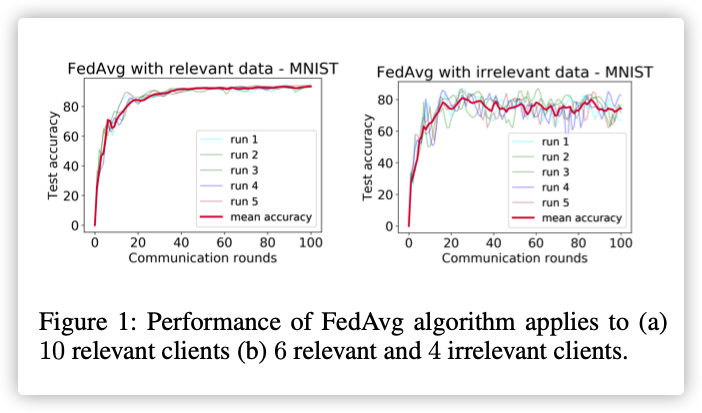
We apply standard FedAvg algorithm to two cases:
(a) where all clients possess relevant data
(b) where some clients possess irrelevant data.
从MNIST建立针对偶数学习的模型。
NOTE:将奇数标签改成偶数!
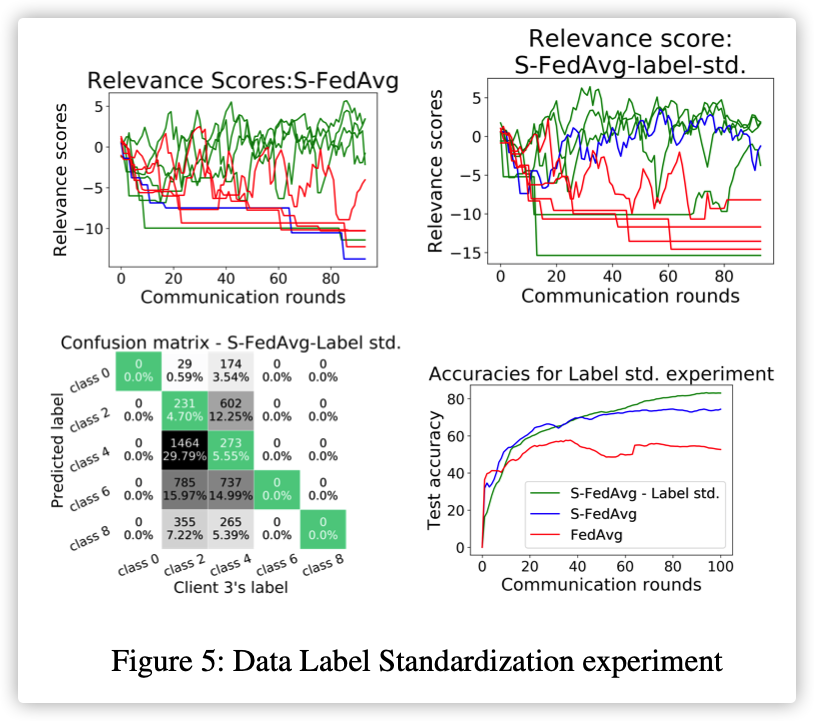
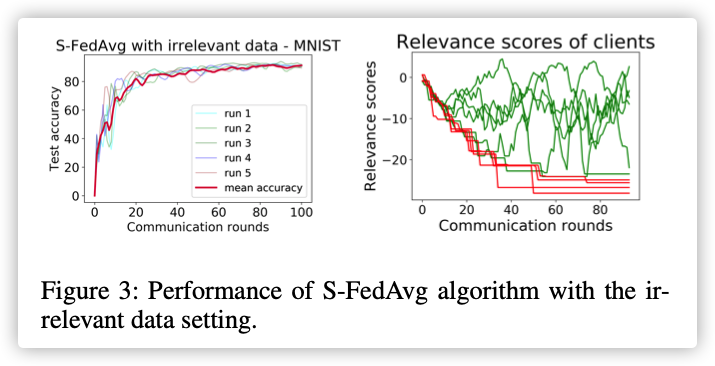
To simulate irrelevance, we work with open-set label noise (Wang et al. 2018) strategy, wherein we randomly flip each odd label of the 4 irrelevant clients to one of the even labels.
Contributions of Our Work:
- 将夏普利值作为衡量设备数据相关性的度量
- 基于夏普利值魔改FedAvg算法(S-FedAvg)
- 解决了两个FRCS问题:
- 选择高质量数据的节点
- 检测和纠正节点的异样数据
0x02 Related Work
0x03 Problem Statement
无关数据的存在使模型准确性和稳定性都下降!
0x04 Proposed Solution
博弈基础
夏普利值定义如下:
其中:是特征函数(贡献值函数);是个参与者全排列(入场顺序);,是在排列中的位置。
通俗理解:就是还没入场前的合作联盟。
考虑全部参与者皆会入场(全排列),上式改下如下:
公式注解:
此时表示的是一个联盟,而不是一个排列。
一个联盟就会存在入场顺序,此处就是用联盟遍历排列的过程。
假设,取,就会存在以下排列:
由于在上述排列的过程中,都是第三个入场的,所以值是相同的。
相同个数是:在左边,其余在右边的情况总数。
相关度得分的计算流程:
-
训练节点将参数更新发送至服务器;
-
定义合作游戏,其中,是特征函数;
代表中央模型参数在验证数据集上的性能.
-
令表示相关度向量,其中表示的相关度。(只保留在服务器,初始化为)
We posit that more the relevance value for a client, more is its likelihood to be relevant and thereby more is its contribution to the objective of central model.
-
每轮聚合时,从合作游戏中获得夏普利值,更新相关度向量:
-
使用计算相对相关度,依据选取参与训练节点集
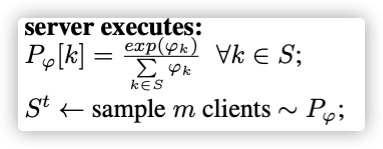
具体算法:


实验中,;可以使用多阶马尔科夫计算。
0x05 Experiments
1.Setup
- Extreme 1-class-non-iid
As is typical with the federated learning setting, we assume that the data is distributed non-iid with each client. We follow the extreme 1-class-non-iid approach mentioned in (Zhao et al. 2018b) while distributing the data to clients.
-
-
验证无关数据的干扰,改变了奇数的label,规则如下:
-
Hyper-parameter Values:

2.S-FedAvg: To Selects Relevant Clients
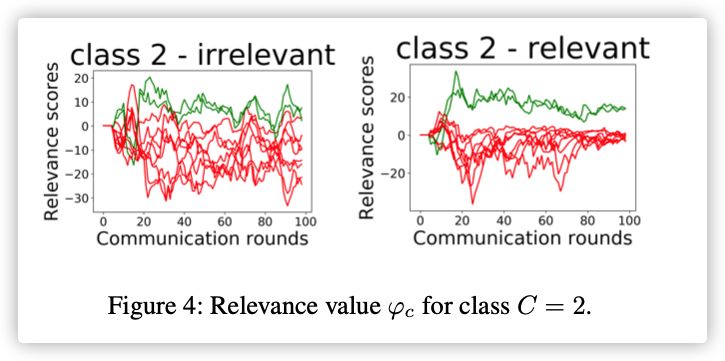
3.Class-specific Best Client Selection
为了检测最好的客户端,将验证集设置成目标数据集。
若想检测出拥有样本最好的训练节点,就将设置成的数据集:
4.Data Label Standardization
本实验将的label: