Reinforcement Learning ZouWei(II)

参考书籍 邹伟博士的《强化学习》

此篇笔记用于整理知识，因此全部基于个人理解…

0x07 值函数逼近

存在状态连续(或数目很多)的情况，这是存储表格已经不现实了。 注意：此时只是说状态数目多，未提及动作！

所以在想能不能设置一个函数，根据输入状态返回值？通过训练这个函数的参数，实现更新表的功能。

因此引入值函数逼近：

$$V(s) = \hat{V}(s,\theta)\\ Q(s,a) = \hat{Q}(s,a,\theta)\\$$

逼近又分为线性逼近和非线性逼近：

函数逼近
	|------线性逼近
	|			|---增量法逼近
	|			|---批量法逼近
	|
	|------非线性逼近
				|---DQN
				|---Double DQN
				|---Dueling DQN

线性逼近

线性逼近就是将值函数表示为状态或者状态函数的线性组合，如：

$$\hat{V}(\boldsymbol{s},\boldsymbol{\theta}) =\boldsymbol{\theta}^T\boldsymbol{x}(s)=\sum_{i=1}^d \theta_i x_i(s)$$

其中$\boldsymbol{\theta}$ 为参数向量，$x(s)$为基函数，常见基函数有多项式基函数、傅里叶基函数。

增量法逼近

使学到的值函数尽可能的逼近真实的值函数，近似度常用最小二乘误差来度量：

$$E_{\theta} = E_{\pi}[(V_{\pi}(s)-\theta^Tx(s))^2]$$

采用梯度下降法，对误差求负导数：

$$-\frac{\partial E_{\theta}}{\partial \theta}=E_{\pi}[2(V_{\pi}(s)-\theta^Tx(s))x(s)]$$

于是得到参数更新规则：

$$\nabla \theta = \alpha(V_{\pi}(s)-\theta^Tx(s))x(s)$$

根据值函数计算的方式不同，又有以下几种情况：

• 基于蒙特卡罗方法的参数逼近：

  $$\nabla \theta = \alpha(G_t-\theta^Tx(s_t))x(s_t)$$

• 基于时序差分法的参数逼近：

  $$\nabla \theta = \alpha(R_{t+1}+\gamma \hat{V}(S_{t+1},\theta)-\hat{V}(S_{t},\theta))\nabla_{\theta}\hat{V}(S_t,\theta) =\alpha(R_{t+1}+\gamma \theta^Tx(s_t)-\theta^Tx(s_{t+1}))x(s_t)$$

• 基于前向TD($\lambda$)的参数逼近：

  $$\nabla \theta = \alpha(G_t^{\lambda}-\hat{V}(S_{t},\theta))\nabla_{\theta}\hat{V}(S_t,\theta) =\alpha(G_t^{\lambda}-\theta^Tx(s_t))x(s_t)$$

• 基于后向TD($\lambda$)的参数逼近：

  $$\delta_t = R_{t+1}+\gamma \theta^Tx(s_{t+1})-\theta^Tx(s_t)\\ E_t=\lambda\gamma E_{t-1}+\nabla_{\theta}\hat{V}(S_t,\theta)=\lambda\gamma E_{t-1}+x(s_t)\\ \nabla \theta = a\delta_tE_t$$

---

但是有时需要对状态动作值函数进行逼近，则$x(s)\rightarrow x(s,a)$

• 基于Sarsa的参数逼近：

$$\nabla \theta = \alpha(R_{t+1}+\gamma\theta^Tx(s_{t+1},a_{t+1})-\theta^Tx(s_{t},a_{t}))x(s_{t},a_{t})$$

• 基于Q-Learning的参数逼近：

  $$\nabla \theta=\alpha(R_{t+1}+\gamma\theta^Tx(s_{t+1},\pi(s_{t+1}))-\theta^Tx(s_{t},a_{t}))x(s_{t},a_{t})$$

批量法逼近

增量法虽然简单但随机性较高，不能充分利用样本，因此引入批量法~

批量法是把一段时间内的数据集中起来，假设一定时间内的数据集为$D=\{(s_1,V^{\pi}_1),(s_2,V^{\pi}_2)...(s_T,V^{\pi}_T)\}$。通过学习，进行函数拟合，满足损失函数$L$最小：

$$L(\theta) = \sum_{t=1}^T(V^{\pi}_t-\theta^Tx(s_t))^2$$

对$\theta$进行求导，使导数为0：

$$-\frac{\partial L(\theta)}{\partial \theta}=2\sum_{t=1}^T(V^{\pi}_t-\theta^Tx(s_t))x(s_t)=0$$

• 最小二乘蒙特卡罗方法参数为：

  $$\alpha\sum_{t=1}^T(G_t-\theta^Tx(s_t))x(s_t)=0\\ \theta = (\sum_{t=1}^Tx(s_t)x(s_t)^T)^{-1}\sum_{t=1}^Tx(s_t)G_t$$

• 最小二乘时序差分方法：

  $$\alpha\sum_{t=1}^T(R_{t+1}+\gamma \theta^Tx(s_{t+1})-\theta^Tx(s_t))x(s_t)=0\\ \theta = (\sum_{t=1}^Tx(s_t)(x(s_t)-\gamma x(s_{t+1}))^T)^{-1}\sum_{t=1}^Tx(s_t)R_{t+1}$$

• 最小二乘前向TD($\lambda$)方法：

  $$\alpha\sum_{t=1}^T(G^{\lambda}_t-\theta^Tx(s_t))x(s_t)=0\\ \theta = (\sum_{t=1}^Tx(s_t)x(s_t)^T)^{-1}\sum_{t=1}^Tx(s_t)G^{\lambda}_t$$

• 最小二乘后向TD($\lambda$)方法：

  $$\alpha\delta_t E_t = 0\\ \theta = (\sum_{t=1}^TE_t(x(s_t)-\gamma x(s_{t+1}))^T)^{-1}\sum_{t=1}^TE_tR_{t+1}$$

• 最小二乘Sarsa方法（基于Q函数）：

  $$\alpha\sum_{t=1}^T(R_{t+1}+\gamma \theta^Tx(s_{t+1},a_{t+1})-\theta^Tx(s_t,a_t))x(s_t,a_t)=0\\ \theta = (\sum_{t=1}^Tx(s_t,a_t)(x(s_t,a_t)-\gamma x(s_{t+1},a_{t+1}))^T)^{-1}\sum_{t=1}^Tx(s_t,a_t)R_{t+1}$$

• 最小二乘Q-learning方法（基于Q函数）：

  $$\alpha\sum_{t=1}^T(R_{t+1}+\gamma \theta^Tx(s_{t+1},\pi(s_{t+1}))-\theta^Tx(s_t,a_t))x(s_t,a_t)=0\\ \theta = (\sum_{t=1}^Tx(s_t,a_t)(x(s_t,a_t)-\gamma x(s_{t+1},\pi(s_{t+1}))^T)^{-1}\sum_{t=1}^Tx(s_t,a_t)R_{t+1}$$

非线性逼近

线性逼近

DQN方法

• 与Q-learning思想一致，可以理解成Q-Learning的深度学习版

• 使用深度神经网络提取特征，近似行为值函数(Q函数)

• 利用经验回放进行训练

• 设置两套网络：TD目标网络、动作值函数逼近网络

  使用梯度更新方式如下：

  $$\theta_{t+1} = \theta_t + \alpha(r+\gamma \mathop{max}_{a'}Q(s',a;\theta_t)-Q(s,a;\theta_t)) \nabla Q(s,a;\theta_t)$$

  这样就导致行为值Q与目标值用得是同一个网络，这样就存在很大的关联性。因此引入一个目标网络，目标值网络需要由动作值函数网络周期性更新：

  $$\theta_{t+1} = \theta_t + \alpha(r+\gamma \mathop{max}_{a'}Q(s',a';\theta_t^-)-Q(s,a;\theta_t)) \nabla Q(s,a;\theta_t)$$

PS:此时可以理解成，对参数的更新就是对网络的更新！

Target网络的更新方式：

• 直接赋值：$\theta^-=\theta$
• 逐渐更新：$\theta^-=(1-\tau)\theta^-+\tau \theta$

Double DQN方法

研究学者发现，DQN和Q-Learning都会过高估计Q值，存在过优化的问题！以DQN为例：

$$a^* = \mathop{argmax}_{a}Q(s_{t+1},a;\theta^-_t)\\ Y^{DQN}_t = R_{t+1} + \gamma \mathop{max}_{a}Q(s_{t+1},a;\theta^-_t)$$

在DQN的过程中，存在选择行为和评估行为是同一个网络,以及同一个值函数~

Double DQN(DDQN) 分别采用不同的值函数来实现动作选择和评估：

$$Y^{DDQN}_t = R_{t+1} + \gamma Q(s_{t+1},\mathop{argmax}_{a}Q(s_{t+1},a;\theta_t);\theta^-_t)$$

Dueling DQN方法

有些时候，影响下一状态的不仅仅是所选动作，还可能是当前状态！

比如单车已经非常倾斜了、不管怎么调整，下一秒都会倒下，此时当前状态对下一状态的影响更大！

因此提出将Q值分解为价值(Value)和优势(Advantage)：

$$Q(s,a) = V(s) + A(s,a)$$

通俗理解,$V(s)$可以理解为该状态$s$下所有动作值函数乘以该动作的概率之和，即动作值函数关于动作概率的期望。所以$Q(s,a)-V(s)$就表示当前动作对于其他动作的优势。

• Dueling DQN的思路：

  把Q网络(求取Q值的神经网络)的结构显式地约束成两部分之和：更动作无关的状态值函数$V(s)$，与在该状态下各个动作的优势函数$A(s,a)$。

• Dueling DQN结构图：

  

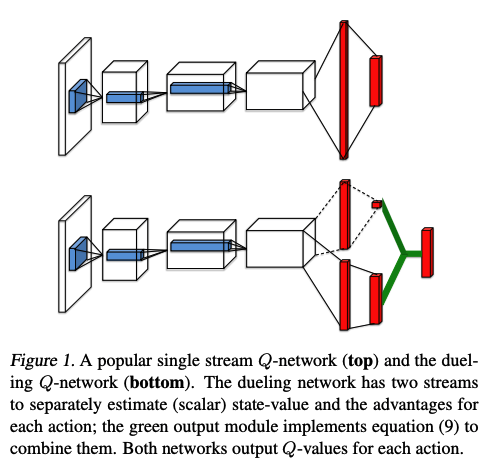
• 网络参数，$\theta$为卷积网络参数，$\alpha,\beta$分别为全连接层网络参数：

  $$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + A(s,a;\theta,\alpha)$$

• New Problem：

  上述等式中，存在两个未知数，这样就会出现一个无法识别的问题：给定一个Q,无法得到唯一的V和A (比如V和A同时加/减 相同的量)，于是就有如下改进：

  $$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + (A(s,a;\theta,\alpha) - \mathop{max}_{a'} A(s,a';\theta,\alpha))$$

  上述等式就能唯一确定V和A，但是实际使用中，更倾向于下面的等式：

  $$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + (A(s,a;\theta,\alpha) - \frac{1}{|A|}\sum_{a'} A(s,a';\theta,\alpha))$$

  这样缩小了Q的范围，去除多余的自由度，提高算法的稳定性！