参考书籍 邹伟博士的《强化学习》

此篇笔记用于整理知识，因此全部基于个人理解…

0x01 基础概念

什么是强化学习？

  • 学习&规划

    前者是指智能体未知环境模型，需要不断与环境进行交互，不断改进策略

    后者是指已知大部分环境模型，智能体不再与环境进行交互，根据状态转移概率和回报，不断进改进策略

  • 探索&利用：

    探索未曾尝试的决策，主要体现在强化学习算法中的随机策略。

    利用已收集的知识，主要体现在一些算法的贪心策略。

  • 预测和控制

    又叫评估与改善。

    分别对应强化学习的打分阶段和策略改善阶段。

0x02 马尔可夫决策

马尔可夫性：下一时间步的状态s′s'，仅与当前时间步的状态ss和所选动作aa相关，与之前的状态、动作无关。

马尔可夫决策五元组:<S,A,R,P,γ><S,A,R,P,\gamma>

贝尔曼方程：

状态值函数的数学表示如下，其中GtG_t是指到结尾的累计收益：

Vπ(s)=Eπ[Gt∣St=s]=Eπ[Rt+1+γRt+2+...∣St=s]V_{\pi}(s) = \mathbb{E}_{\pi}[G_t|S_t=s] = \mathbb{E}_{\pi}[R_{t+1}+\gamma R_{t+2}+...|S_t=s]

对其进行公式推导：

Vπ(s)=Eπ[Gt∣St=s]=Eπ[Rt+1+γRt+2+γ2Rt+3+...∣St=s]=Eπ[Rt+1+γ(Rt+2+γRt+3...)∣St=s]=Eπ[Rt+1+γGt+1∣St=s]=Eπ[Rt+1+γVπ(St+1)∣St=s]\begin{aligned} V_{\pi}(s) =& \mathbb{E}_{\pi}[G_t|S_t=s] \\ =& \mathbb{E}_{\pi}[R_{t+1}+\gamma R_{t+2}+\gamma ^2R_{t+3}+...|S_t=s]\\ =& \mathbb{E}_{\pi}[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}...)|S_t=s]\\ =& \mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ =& \mathbb{E}_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1})|S_t=s]\\ \end{aligned}

同理：

Qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[Rt+1+γQπ(St+1,At+1)∣St=s,At=a]\begin{aligned} Q_{\pi}(s,a) =& \mathbb{E}_{\pi}[G_t|S_t=s,A_t=a] \\ =& \mathbb{E}_{\pi}[R_{t+1}+\gamma Q_{\pi}(S_{t+1},A_{t+1})|S_t=s,A_t=a]\\ \end{aligned}

以上是贝尔曼方程的最初形态，又因为状态值函数与行为值函数之间的关系：

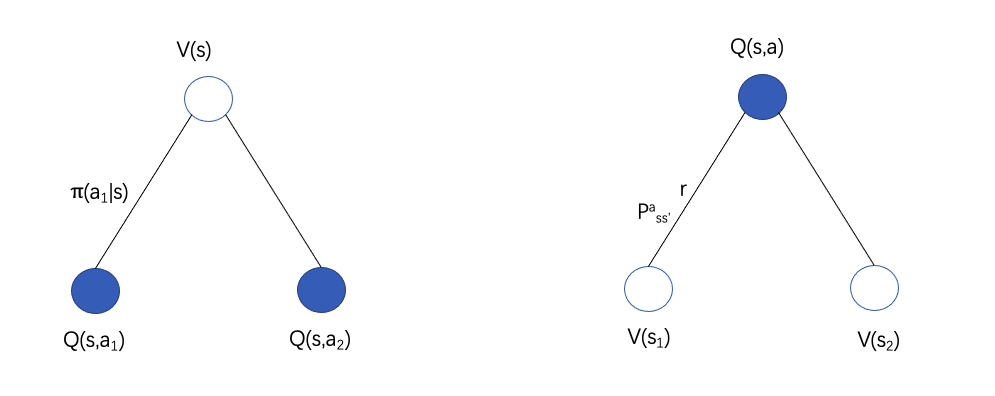
则又有以下形式:

Vπ(s)=∑a∈Aπ(a∣s)Qπ(s,a)V_{\pi}(s)=\sum_{a\in A}\pi(a|s)Q_{\pi}(s,a)

Qπ(s,a)=Rsa+γ∑s′∈SPss′aVπ(s′)Q_{\pi}(s,a)=R_{s}^a + \gamma \sum_{s' \in S}P^a_{ss'}V_{\pi}(s')

Vπ(s)=∑a∈Aπ(a∣s)(Rsa+γ∑s′∈SPss′aVπ(s′))V_{\pi}(s) = \sum_{a\in A} \pi(a|s)(R_{s}^a + \gamma \sum_{s' \in S}P^a_{ss'}V_{\pi}(s'))

Qπ(s,a)=Rsa+γ∑s′∈SPss′a∑a′∈Aπ(a′∣s′)Qπ(s′,a′)Q_{\pi}(s,a) =R_{s}^a + \gamma \sum_{s' \in S}P^a_{ss'}\sum_{a'\in A}\pi(a'|s')Q_{\pi}(s',a')

0x03 动态规划

此部分不是重点

属于规划的范畴，即模型状态转移概率PP是已知的，

0x04 蒙特卡罗 MC

未知模型，即转移概率PP未知

核心思想：在问题领域进行随机抽样，通过不断、反复、大量的抽样后，统计结果，得到解空间上关于问题领域的接近真实的分布。

执行TT步的一条完整轨迹如下：

<s0,a0,r0,s1,a1,r1,...sT,aT,rT><s_0,a_0,r_0,s_1,a_1,r_1,...s_T,a_T,r_T>

为了计算方便，使用累计回报GntG_{nt}代替立即回报，nn表示第nn个轨迹：

<s0,a0,G11,s1,a1,G12,...sT,aT,G1T><s_0,a_0,G_{11},s_1,a_1,G_{12},...s_T,a_T,G_{1T}>

估算每个状态的状态值V(s)V(s)时有两种方式(处理一条轨迹中出现多次的相同状态的情况，即转圈情况)：

  • 初次访问：相同状态的累计回报只计算第一次
  • 每次访问：每次经过都计算

V(s)=G12+G2k+...N(s)V(s)=\frac{G_{12}+G_{2k}+...}{N(s)}

其中N(s)N(s)表示所有轨迹中ss出现的总次数，两者的区别就是分子是否有重复场景的情况。

MC的主要形式：估计行为值函数Q代替估计值函数V

Q(s1,a1)=G12+...N(s1,a1)Q(s_1,a_1)=\frac{G_{12}+...}{N(s_1,a_1)}

其中N(s,a)N(s,a)表示所有轨迹中状态行为对(s,a)(s,a)出现的总次数，再结合增量更新方法：

Q(st,at)←Q(st,at)+α(Gt−Q(st,at))Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha (G_t-Q(s_t,a_t))

0x05 时序差分 TD

MC计算的时候需要累积回报均值GtG_t，这就需要知道完整的轨迹（到终止状态）

但是存在未知完整轨迹或无终止状态的情况，因此引入时序差分。

因此实际情况中，主要使用TD值函数更新方式。

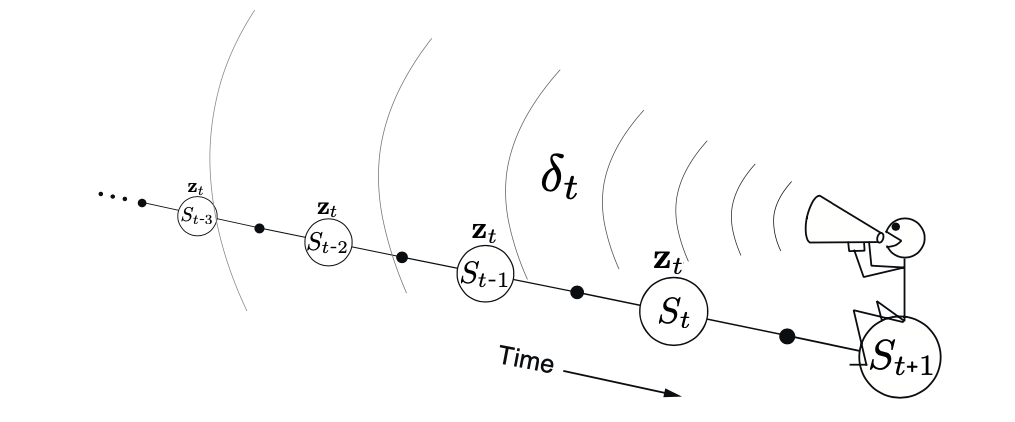
主要思想：在估计状态StS_t的值函数时，用的是离开该状态的立即回报Rt+1R_{t+1}和下一状态St+1S_{t+1}的预估折扣值γV(St+1)\gamma V(S_{t+1})之和，即：

Vπ(St)=Eπ[Gt∣St=s]=Eπ[Rt+1+γV(St+1)∣St=s]V_{\pi}(S_t) = \mathbb{E}_{\pi}[G_t|S_t=s] = \mathbb{E}_{\pi}[R_{t+1}+\gamma V(S_{t+1})|S_t=s]

于是TD的值函数更新方式：

V(st)←V(st)+α(Rt+1+γV(st+1)−V(st))V(s_t)\leftarrow V(s_t) + \alpha(R_{t+1}+\gamma V(s_{t+1})-V(s_t))

其中：Rt+1+γV(st+1)R_{t+1}+\gamma V(s_{t+1}) 称为TD目标值，$\delta_t = R_{t+1}+\gamma V(s_{t+1})-V(s_t) $称为TD误差。

这种方法也叫TD(0)TD(0)是TD(λ)TD(\lambda)的一种特殊形式。

Saras算法：

Q(s,a)←Q(s,a)+α(R+γQ(s′,a′)−Q(s,a))Q(s,a) \leftarrow Q(s,a)+\alpha(R+\gamma Q(s',a')-Q(s,a))

Q-Learning算法：

Q(s,a)←Q(s,a)+α(R+γ maxa′Q(s′,a′)−Q(s,a))Q(s,a) \leftarrow Q(s,a)+\alpha(R+\gamma\ \mathop{max}_{a'} Q(s',a')-Q(s,a))

0x06 资格迹

MC和TD的一个区别是，基于当前状态往未来看的距离不同。

MC：一直观测到结束，整个长度记为NN。

TD: 长度是1，只参考了下一个状态的状态值。

能否够构造长度为d,(1≤d≤N)d,(1\leq d\leq N)的值估计方法呢?

因此引入多步时序差分法（也叫资格迹法）

Gtn=rt+1+γrt+2+γ2rt+3+...+γn−1rt+n+γnV(st+n)G_t^n = r_{t+1}+\gamma r_{t+2} +\gamma^2 r_{t+3}+...+\gamma^{n-1}r_{t+n}+\gamma^nV(s_{t+n})

但是存在两种视角：

  • 前向视角：

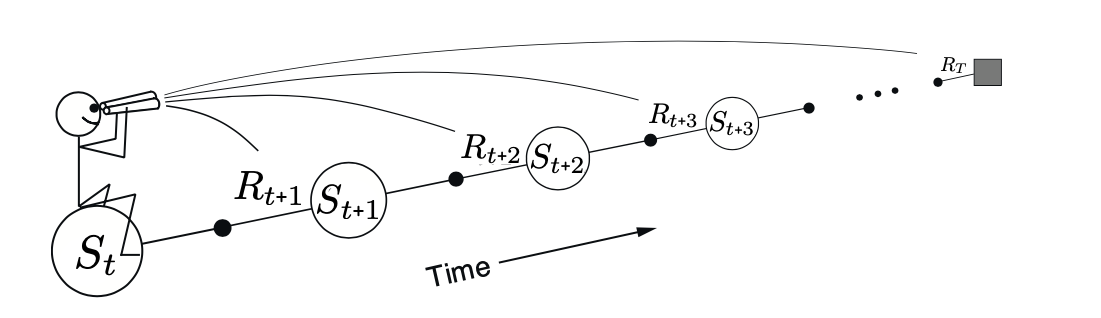
​ 前向视角又叫理论视角，使用n个值来更新状态值，保证其权值和为1(资格迹的体现)。

  • 后向视角：

    在后向视角中，资格迹就是进行资格进行分配，也可以理解成权值的一种分配情况。

TD(λ\lambda)前向算法

Gtλ=(1−λ)∑n=1∞λn−1GtnG_{t}^{\lambda} = (1-\lambda)\sum_{n=1}^{\infin} \lambda^{n-1}G^n_t

如果轨迹长度为TT，则有(保证权重和为1)：

Gtλ=(1−λ)∑n=1T−t−1λn−1Gtn+λT−t−1GtG_{t}^{\lambda} = (1-\lambda)\sum_{n=1}^{T-t-1} \lambda^{n-1}G^n_t+\lambda^{T-t-1}G_t

值函数更新如下：

V(st)←V(st)+α(Gtλ−V(st))V(s_t) \leftarrow V(s_t) + \alpha(G^{\lambda}_t - V(s_t))

TD(λ\lambda)后向算法

资格迹需要考虑，导致这一状态产生的原因是多少来自频率、多少来自最近状态。

例如：连续三次拳击，接着一次电击，导致小狗死亡。

那小狗死亡原因，电击和拳击如何分配？

在tt时刻的状态ss对应的资格迹，记为Et(s)E_t(s):

E0(s)=0E_0(s)=0

Et(s)=γλEt−1(s)+I(St=s)E_t(s) = \gamma \lambda E_{t-1}(s) + I(S_t=s)

此方式被称为累计型资格迹，即状态被访问时，资格进行累加，不访问时退化。

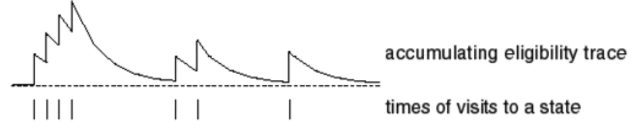
除了累计型资格迹，还有代替性资格迹:

Et(S)={γλEt−1(s),st≠s1,st=s\begin{aligned} E_t(S) = \left\{ \begin{array}{l} \gamma \lambda E_{t-1}(s),s_t\neq s\\ 1,s_t=s \end{array} \right. \end{aligned}

TD误差更新如下:

δt=Rt+1+γVt(St+1)−Vt(St)\delta_t = R_{t+1} + \gamma V_t(S_{t+1})-V_t(S_t)

再结合资格迹更新状态价值，则有：

V(s)←V(s)+αδtEt(s)V(s) \leftarrow V(s) + \alpha\delta_tE_t(s)

Sarsa(λ\lambda) (后向)算法：

与传统的TD(λ)TD(\lambda)的不同之处是，本算法使用行为值函数：

本章访问状态时，资格迹+1+1主要是因为表格型问题，状态动作集合是可数的。