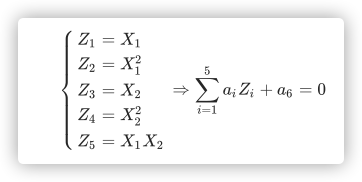核方法

0x01 为什么需要核函数

问题1：

SVM显然是线性分类器，但数据如果根本就线性不可分怎么办？

解决方案1：

数据在原始空间（称为输入空间）线性不可分，但是映射到高维空间（称为特征空间）后很可能就线性可分了。

问题2：

映射到高维空间同时带来一个问题：在高维空间上求解一个带约束的优化问题显然比在低维空间上计算量要大得多，这就是所谓的“维数灾难”。

解决方案2：

于是就引入了“核函数”，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就是说避免了直接在高维空间中的复杂计算

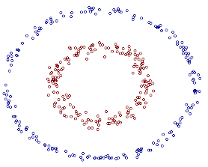
例如图中的两类数据，分别分布为两个圆圈的形状，不论是任何高级的分类器，只要它是线性的，就没法处理，SVM 也不行。因为这样的数据本身就是线性不可分的。

0x02 什么是核函数

引入:

从上图我们可以看出一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：

$a_1X_1+a_2X_1^2+a_3X_2+a_4X_2^2+a_5X_1X_2+a_6=0$

注意上面的形式，如果我们构造另外一个五维的空间:

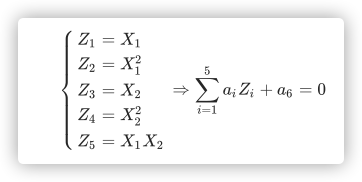
核方法的主要思想是基于这样一个假设：“在低维空间中不能线性分割的点集，通过转化为高维空间中的点集时，很有可能变为线性可分的”

$\sum_{i=1}^5 a_iZ_i +a_6=0$

核函数的定义：

设 $\mathcal{X}$ 是输入空间(欧式空间 $R^n$ 的子集或离散集合)，又设 $\mathcal{H}$ 为特征空间(希尔伯特空间)，如果存在一个从 $\mathcal{X}$ 到 $\mathcal{H}$ 的映射：

$\phi(x):\mathcal{X} \rightarrow \mathcal{H}$

使得对所有的 $x,z \in \mathcal{X}$ ,函数 $K(x,z)$ 满足条件：

$K(x,z) = \phi(x)\cdot\phi(z)$

则称 $K(x,z)$ 为核函数， $\phi(x)$ 为映射函数，式中$ \phi(x)\cdot\phi(z)$为二者内积。

核技巧一种利用核函数直接计算 $K(x,z)$ ，以避开分别计算 $\phi(x)$ 和 $\phi(z)$ ，从而加速核方法计算的技巧。

映射函数 $\phi$ 的取法并不是唯一的：

假设输入空间是 $R^2$ ,核函数是 $K(x,z)=(x\cdot z)^2$ ,试找出相关的特征空间 $\mathcal{H}$ 和映射 $\phi(x):R^2 \rightarrow \mathcal{H}$ 。

解：

取特征空间 $\mathcal{H}=R^3$ ,记 $x=(x^{(1)},x^{(2)})^T,z=(z^{(1)},z^{(2)})^T$ .由于

$(x\cdot z)^2 = (x^{(1)}z^{(1)}+x^{(2)}z^{(2)})^2 = (x^{(1)}z^{(1)})^2+2x^{(1)}z^{(1)}x^{(2)}z^{(2)}+(x^{(2)}z^{(2)})^2$

所以可以取映射函数 $\phi(x)=((x^{(1)})^2,\sqrt{2}x^{(1)}x^{(2)},(x^{(2)})^2)^T$ .

也可以取 $\phi(x)=\frac{1}{\sqrt{2}}((x^{(1)})^2-(x^{(2)})^2,2x^{(1)}x^{(2)},(x^{(1)})^2+(x^{(2)})^2)^T$ .

但取 $\mathcal{H}=R^4$ 时，可以取 $\phi(x)=((x^{(1)})^2,x^{(1)}x^{(2)},x^{(1)}x^{(2)},(x^{(2)})^2)^T$

0x03 正定核

预备知识：

假设 $K(x,z)$ 是定义在 $\mathcal{X}×\mathcal{X}$ 上的对称函数，对任意的 $x_i\in \mathcal{X},i=1,2,3,...,m,K(x,z)$ 关于 $x_1,x_2,...,x_m$ 的Gram矩阵是半正定的。则依据函数 $K(x,z)$ 可以构成一个希尔伯特空间。其步骤如下：

首先定义映射 $\phi$ 并构成向量空间 $\mathcal{S}$ .
在 $\mathcal{S}$ 定义内积构成内积空间.
将 $\mathcal{S}$ 完备化成希尔伯特空间.

1.定义映射，构成向量空间 $\mathcal{S}$ .

定义映射:

$\phi：x \rightarrow K(\cdot,x)$

根据这一映射，对任意 $x_i \in \mathcal{X},\alpha_i \in R$ ,定义线性组合：

$f(\cdot)=\sum_{i=1}^m\alpha_iK(\cdot,x_i) \tag{1}$

已知线性组合的各个元素均来自集合 $\mathcal{S}$ 。由于集合 $\mathcal{S}$ 对加法和乘法运算是封闭的，所以 $\mathcal{S}$ 构成一个向量空间。

2.在 $\mathcal{S}$ 定义内积构成内积空间.

在 $\mathcal{S}$ 上定义一个运算 $*$ ,对任意的 $f,g\in \mathcal{S}$ ,

$g(\cdot)=\sum_{j=1}^l\beta_jK(\cdot,z_j) \tag{2}$

定义运算 $*$ :

$f*g = \sum_{i=1}^m\sum_{j=1}^l\alpha_i\beta_jK(x_i.z_j) \tag{3}$

证明运算 $*$ 是空间 $\mathcal{S}$ 的内积。需要证：

$\begin{array}{l} a.&(cf)*g=c(f*g),c\in R\\ b.&(f+g)*h=f*h+g*h,h\in \mathcal{S}\\ c.&f*g=g*f\\ d.&f*f\geq0,f*f=0 ⇔ f=0 \end{array}$

其中a.b.c易证。现在主要证明d.

现证明 $f*f\geq0$ :

由式(3)可得：

$f*f=\sum_{i,j=1}^m\alpha_i\alpha_jK(x_i.x_j)$

由Gram矩阵的半正定性知该式右端非负，即 $f*f\geq0$ .

再证明 $f*f=0 ⇔ f=0$ :

充分性显然成立。下面工作主要是证明必要性，即 $f*f=0 ⇒ f=0$ .

首先证明不等式：

$|f*g|^2\leq(f*f)(g*g) \tag{4}$

设 $f,g\in \mathcal{S},\lambda \in R$ ,则 $f+\lambda g\in\mathcal{S}$ ,于是：

$(f+\lambda g)(f+\lambda g)\geq0\\ f*f+2\lambda(f*g)+\lambda^2(g*g)\geq0$

将其看作 $\lambda$ 的二次函数，根据根的判别式可知：

$(f*g)^2-(f*f)(g*g)\leq0$

则式(4)得证。

取 $g=K(\cdot,x)$ ，则由式(3)可得： $K(\cdot,x)*f=\sum_{i=1}^m\alpha_iK(x,x_i)=f(x)$ .所以有：

$|f(x)|^2=|K(\cdot,x)*f|^2 \tag{5}$

结合式(4)可知：

$|K(\cdot,x)*f|^2\leq(K(\cdot,x)*K(\cdot,x))(f*f)=K(x,x)(f*f)$

即 $|f(x)|^2\leq K(x,x)(f*f)$ 。

此式表明， $f*f=0$ 时，对任意的 $x\in \mathcal{X}$ ,都有 $|f(x)|=0$ .

至此证明了 $*$ 是向量空间 $\mathcal{X}$ 的内积，可以用 $\cdot$ 代替 $*$ :

$f\cdot g = \sum_{i=1}^m\sum_{j=1}^l\alpha_i\beta_jK(x_i.z_j) \tag{6}$

3.将 $\mathcal{S}$ 完备化成希尔伯特空间.

由式(6)定义的内积就可以得到范数:

$||f||=\sqrt{f\cdot f}$

因此， $\mathcal{S}$ 是一个赋范向量空间。根据泛函分析理论，对于不完备的赋范向量空间 $\mathcal{S}$ ,一定可以使之完备化，得到完备的赋范向量空间 $\mathcal{H}$ 。一个内积空间，当作为赋范向量空间是完备的时候，就是希尔伯特空间。

扩展：

完备性

完备性就是说任意柯西列的极限仍然在这个空间中。

柯西列就是空间中元素构成的一个序列，并且这个序列在无穷远处两个元素之间的距离趋于零。准确的说，如果空间中有一个序列 $\{x_n\}$ ,当 $n,m\rightarrow \infty$ 的时候， $d(x_n,x_m)\rightarrow 0$ ，则 $\{x_n\}$ 就是一个柯西列，也就是说完备性保证了取序列极限不会跑到空间外面去。

一个不完备的例子就是有理数的集合，例如这个集合可以用柯西列的极限去逼近 $\sqrt2$ ，而这个极限并不在有理数这个集合中，所以有理数几何是不完备的。

充要条件：

设 $K:\mathcal{X}×\mathcal{X}\rightarrow R$ 是对称函数，则 $K(x,z)$ 为正定核函数的充要条件是对任意的 $x_i\in \mathcal{X},i=1,2,3,...,m,K(x,z)$ 对应的 $Gram$ 矩阵：

$K=[K(x_i,x_j)]_{m×m}$

是半正定矩阵。

必要性：

由于 $K(x,z)$ 是 $\mathcal{X}×\mathcal{X}$ 上的正定核，所以存在从 $\mathcal{X}\rightarrow \mathcal{H}$ 的映射 $\phi$ ，使得 $K(x,z)=\phi(x)\cdot \phi(z)$ .

构造Gram矩阵：

$[K_{ij}]_{m×m}=[K(x_i,x_j)]_{m×m}$

对任意的 $c_1,c_2,...,c_m \in R$ ,有：

$\begin{array}{l} \sum_{i,j=1}^mc_ic_jK(x_i,x_j)&=\sum_{i,j=1}^mc_ic_j(\phi(x)\cdot \phi(z))\\ &=\left( \sum_ic_i\phi(x_i)\right)\cdot\left( \sum_jc_j\phi(x_j)\right)\\ &=||\sum_ic_i\phi(x_i)||^2 \geq 0 \end{array}$

因此 $K(x,z)$ 的Gram是半正定的。

充分性：

假设 $K(x,z)$ 是定义在 $\mathcal{X}×\mathcal{X}$ 上的对称函数，对任意的 $x_i\in \mathcal{X},i=1,2,3,...,m,K(x,z)$ 关于 $x_1,x_2,...,x_m$ 的Gram矩阵是半正定的。可以构造映射函数 $\phi:x\rightarrow K(\cdot,x)$ .

$K(\cdot,x)*f=\sum_{i=1}^m\alpha_iK(x,x_i)=f(x)$

并且 $K(\cdot,x)\cdot K(\cdot,z)=K(x,z)$ 可知： $K(x,z)=\phi(x)\cdot\phi(z)$

表明 $K(x,z)$ 是核函数。

0x04 常见核函数

线性核函数

$K(x,z) = x\cdot z$

线性核，主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的。
多项式核函数

$K(x,z) = (x\cdot z+1)^p$

多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。
高斯核函数

$K(x,z) = exp(-\frac{||x-z||^2}{2\sigma^2})$

高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。
Sigmoid核函数

$K(x,z) = tanh(\gamma x\cdot z+\theta)$

采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。