Proximal Policy Optimization Algorithms

下载链接

0x00 Abstract

传统的数据样本在策略更新后就会失效，本文提出了一种新的目标函数，能够有效利用数据样本、进行多轮更新。

PPO算法与TRPO相比，执行更简单、泛化更好、采样更随机。

KEY WORDS：Reinforcement Learning,PPO,On-Policy

0x01 Introduction

强化学习常见的方法仍有提升的空间：扩展性（大量模型&并行执行）、数据利用率、健壮性。

• Q-Learing：不能解决连续性问题、vanilla 策略梯度数据利用率和健壮性较差；
• TRPO：过于复杂、与部分结构不兼容，如噪声(dropout)、参数共享

本文贡献：

• PPO算法只用一阶优化就可以达到TRPO的数据利用率和相关性能表现。
• 目标函数引入Clip函数（修剪函数）,能够获得算法性能的下界。
• 与其他算法的实验比较显示，性能较好。

0x02 Background: Prolicy Optimization

Policy Gradient Methods

常见的估值函数：

$$\hat{g}=\hat{\mathbb{E}}_t[\triangledown_{\theta} log\pi_{\theta}(a_t|s_t)\hat{A}_t]$$

其中$\hat{A_t}$为优势函数。为了获得上面的梯度，需要的对下面的函数进行求导：

$$L^{PG}(\theta)=\hat{\mathbb{E}}_t[log\pi_{\theta}(a_t|s_t)\hat{A}_t]$$

使用相同数据执行多步更新的时候，往往导致策略更新后效果变差。

Trust Region Methods

TRPO提出的目标函数（替身函数）是一个求最大值的目标函数，并有更新幅度的限制：

$$\mathop{maximize}\limits_{\theta}\ \hat{\mathbb{E}}_t[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta old}(a_t|s_t)}\hat{A}_t]\\ subject\ to\ \hat{\mathbb{E}}_t[KL[\pi_{\theta old}(·|s_t),\pi_{\theta}(·|s_t)]] \leq \delta$$

TRPO使用的是硬性限制而不是惩罚（目标函数添加处罚项），但使用共轭梯度算法是二阶优化算法。

0x03 Clipped Surrogate Objective

令$r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta old}(a_t|s_t)},r_t(\theta_{old})=1$,则TRPO的替身目标函数就是：

$$L^{CPI}(\theta)=\hat{\mathbb{E}}_t[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta old}(a_t|s_t)}\hat{A}_t]=\hat{\mathbb{E}}_t[r_t(\theta)\hat{A}_t]$$

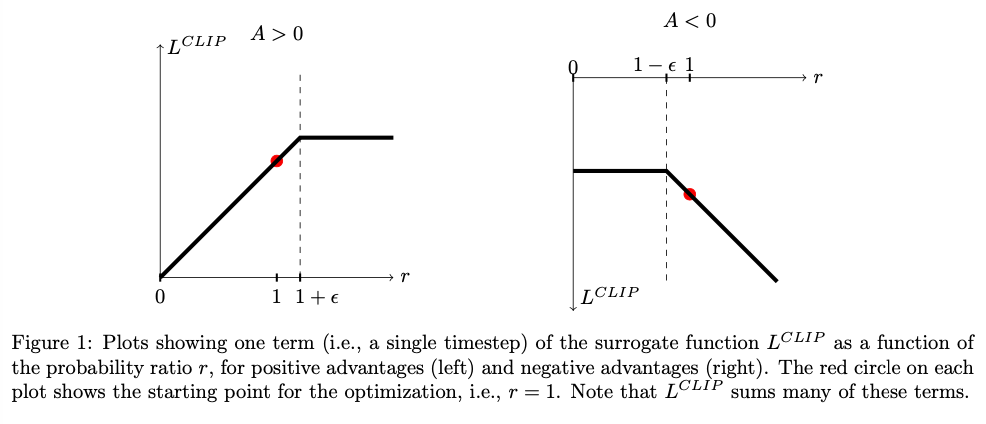
如果不对更新加以限制，会产生大幅度的消极更新，本文对该目标函数添加限制如下：

$$L^{CLIP}(\theta)=\hat{\mathbb{E}}_t[min(r_t(\theta)\hat{A_t},clip(r_t(\theta),1-\epsilon，1+\epsilon)\hat{A_t})$$

效果图如下：

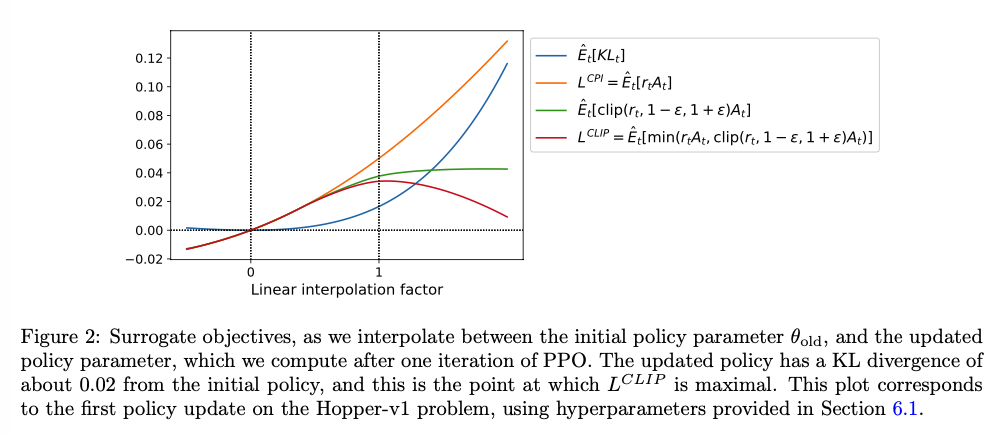
0x04 Adaptive KL Penalty Coefficient

本节是用于凑字数的…

利用KL散度作为惩罚系数，但是效果不如CLIP好：

0x05 Algorithm

引入神经网路使用的目标函数：

$$L^{CLIP+VF+S}_t(\theta)=\hat{\mathbb{E}}_t[L^{CLIP}_t(\theta)-c_1L^{VF}_t(\theta)+c_2S[\pi_{\theta}](s_t)]$$

其中$c_1,c_2$是系数，$S$是熵激励，$L^{VF}_t=(V_{\theta}(s_t)-V^{targ}_t)^2$是二次误差。

前人工作者使用的TD-error型优势函数：

$$\hat{A}_t=-V(s_t)+r_{t}+\gamma r_{t+1}+...+\gamma^{T-t+1}r_{T-1}+\gamma^{T-t}V(s_T)$$

本文引入$\lambda$并修改优势函数如下：

$$\hat{A}_t=\delta_t+(\gamma \lambda)\delta_{t+1}+...+(\gamma\lambda)^{T-t+1}\delta_{T-1},\\ where\ \delta_t=r_t+\gamma V(s_{t+1})-V(s_t)$$

$N$个(并行)actor中的每一个actor收集$T$个数据，进行训练：

0x06 Experiments

0x07 Conclusion

• 多轮随机梯度进行策略更新
• 与TRPO有相同的稳定性和可靠性，但执行更简单，应用范围更广
• 较好的综合性能

Note：

• First-order optimization
• conjugate gradient algorithm（共轭梯度法）