Local SGD Converges Fast and Communicates Little
Question:
Q:为什么SGD降低方差,可以提高收敛速率?
A:方差反应了梯度的波动,因此方差越小,说明梯度越集中,收敛就越快。
0x00 Abstract
受限于网络延迟和带宽限制,多节点的随机梯度下降很难实现收敛的线性加速;Local SGD可以实现,但是缺乏理论证明。
本文证明了Local SGD对凸优化问题的收敛速度,能达到SGD与节点数和批次大小的线性加速关系。通信轮数能减少到(表示总轮数)。Local SGD也可用于异步参数更新。
Local SGD能用于大型深度学习模型的训练。
KEY WORDS: Local SGD,Theoretical, Speedup
0x01 Introduction
SGD的组成:
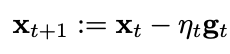
其中的期望就是函数对的求导(是损失函数)。
parallel SGD:
- 用多个节点梯度的平均值,代替
- 每轮节点都要通信交换,通信成为瓶颈
Mini-batch parallel SGD:
- 增加计算-通信比
- 每次通信前,训练mini-batch次(增加分子)
- 当mini-batch太大时,性能会降低
This paper:
- 增加计算-通信比
- 降低通信频率 (减少分母)
- 每个节点可以单独进行参数更新,经过一段时间全局更新一次
- 示例:one-hot SGD等
问题:
- 多久通信一次。(仍未解决)
- 理论上,采用平均值是否对凸优化函数有作用(即,K个节点是否比单节点快K倍)。(本论文)
贡献:
| 字母 | 含义 | 备注 |
|---|---|---|
| 单样本损失 | ||
| 损失函数 | 光滑、强凸 | |
| mini-batch size | ||
| 并行节点数 | ||
| 本地迭代周期 | 本地执行次,上传参数 | |
| 最优解向量(权值) | ||
| 训练轮数 | ||
| 聚合轮标记集合 | , if t in I,aggregation |
|
| 经过轮的聚合参数 |
则本文有以下结论:
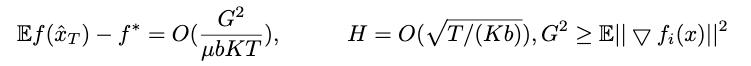
与Parallel SGD对比:减少次聚合通信
与mini-batch SGD对比:实现了线性加速,但需要较少次的通信
增加计算-通信比:增加b、或H,当b和H较小时,可以起到线性加速,不能选择太大。
相关工作:
- 通信前,数据压缩
- 参数异步更新
- 随机平均、非凸问题
0x02 Local SGD
算法过程如下:

减少方差
| 方法 | 收敛速度 | 备注 |
|---|---|---|
| SGD | ||
| Parallel SGD | 为并行度,相关的梯度,线性加速 | |
| Local SGD | ? | 需要证明个独立的梯度序列仍以收敛 |
总体思路:像Parallel SGD 一样,能够减少方差至,即可证明收敛加速。
收敛结果
定理2.2:
收敛速度:在足够大时,local SGD收敛速度是,在K和b上均实现加速。
全局聚合步长:需要设置。
特殊情况:没有考虑优化特殊情况,例如的 one-hot averaging。
时长未知/适应通信频率:优化之初,越多的通信收敛越快;时长未定时(比如训练到指定准确率才会停止),可以提高通信频率。
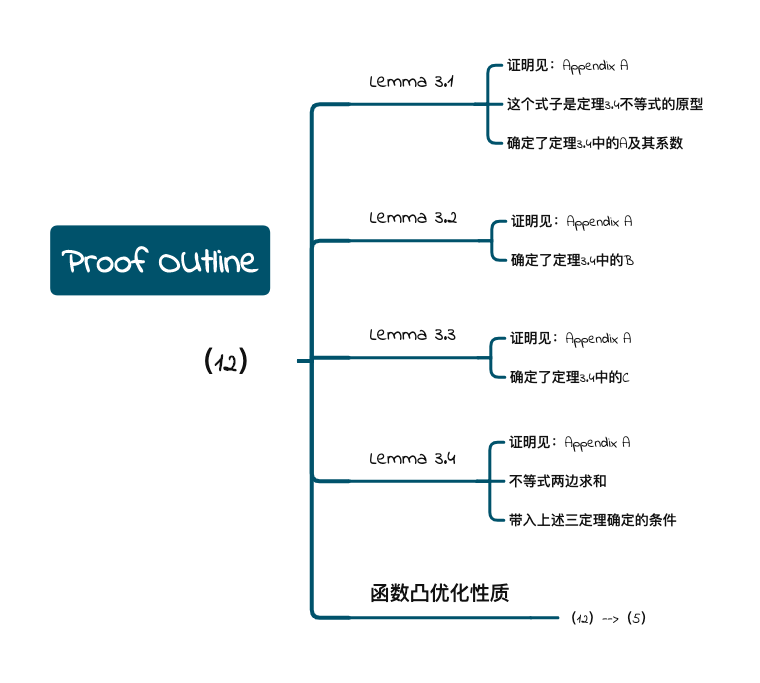
0x03 Proof Outline
这部分是为了证明定理2.2(论文中公式(5))所用的结论,附录A是证明以下用到的4个定理
非常麻烦。。。_(:з」∠)_
由此部分可知上一部分的结论有充分的理论证明(~ ̄▽ ̄)~
0x04 Numberical Illustration
此部分用数据说话。
Speedup
-
由算法1可知,花费的时间由 梯度计算次数和 通信时间共同决定。
-
对于分布式系统中的单个节点,每次通信会传输个向量(一半往外传输,一半接收),会进行次通信。
-
就会得到以下结论:
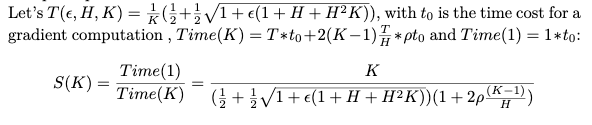
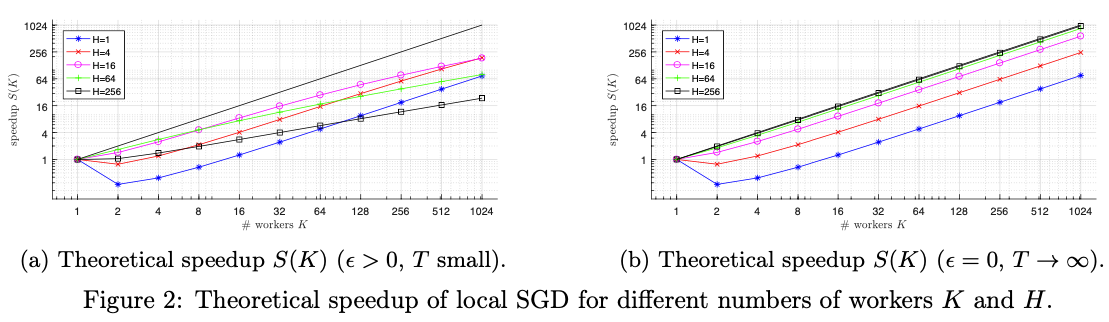
Theoretical
-
增加可以降低并行度的负面影响
-
精度时,才是真正的线性加速,或着足够大 ===>???
不明白精度的意思
Experimental
逻辑回归问题,w8a数据集
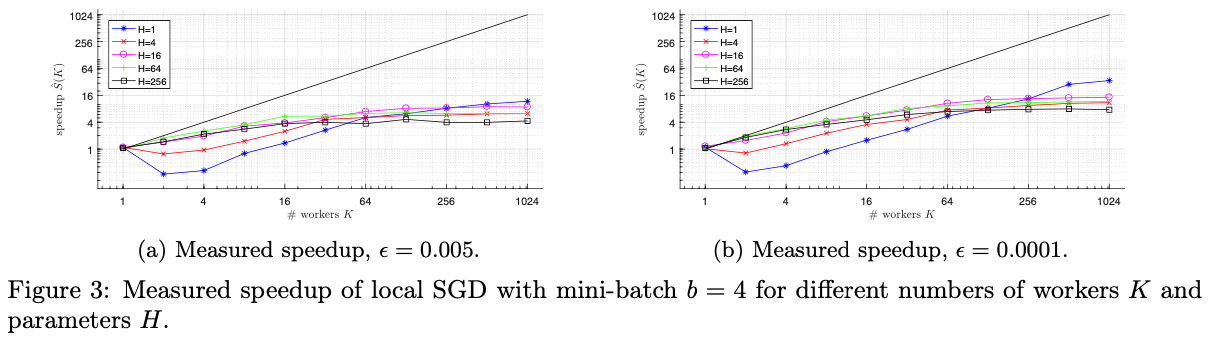
Conclusion
- 对的限制很小,所以可以取得很大
- 较小时,会存在的依赖关系
???和之前的有差别
0x05 Asynchronous Local SGD
此部分说明,适用于异步更新

结论如下:

0x06 Conclusion
- 在强凸文问题,K个节点的Local SGD能实现线性加速
- 与mini-batch 相比,节省了的全局通信轮数
- 未来方向:
- 对偏置、方差的分析
- 取消梯度边界假设、数据相关性
- 非凸问题



