作者：涌井良幸、涌井贞美

译者：杨瑞龙

0x01 神经网络的思想

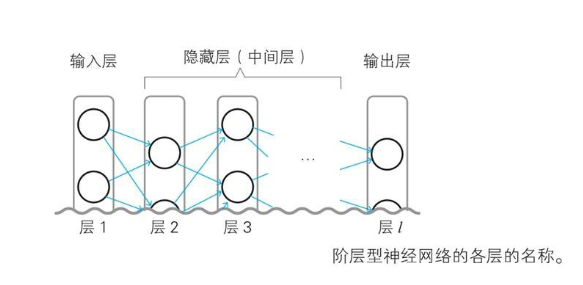
通过生物神经网络等例子引入计算机的神经网络。

输入层–>隐藏层*n–>输出层

0x02 神经网络的数学基础

2-1 神经网络所需函数

一次、二次函数
单位阶跃函数
指数函数和Sigmod函数
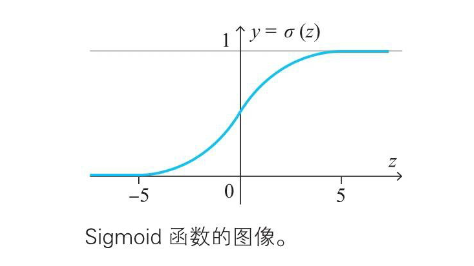
正态分布的概率密度函数

用计算机实际确定神经网络时，必须设定权重和偏置的初始值。求初始值时，正态分布(normal distribution)是一个有用的工具。使用服从这个分布的随机数，容易取得好的结果。

2-2 数列和递推函数

计算机擅长递推，不擅长求导。

误差反向传播就是根据递推关系进行计算的。

2-3、4 ∑符号和向量

具有算数加法的一般性质。
柯西-施瓦兹不等式。
张量是向量的扩展。

2-5 矩阵基础

Hadamard 乘积：哈达玛积，即 $C_{ij}=A_{ij}*B_{ij}$ 。

2-6、7 导数基础和偏导数

Sigmod函数导数： $\sigma'(x) = \sigma(x)*(1-\sigma(x))$

偏导求极值，可以考虑拉格朗日乘数法。

2-8~12 链式法则和梯度下降

单变量、多变量的链式求导发则，是反向传播的基础。

多元近似公式：为求极值。

多元泰勒展开式：

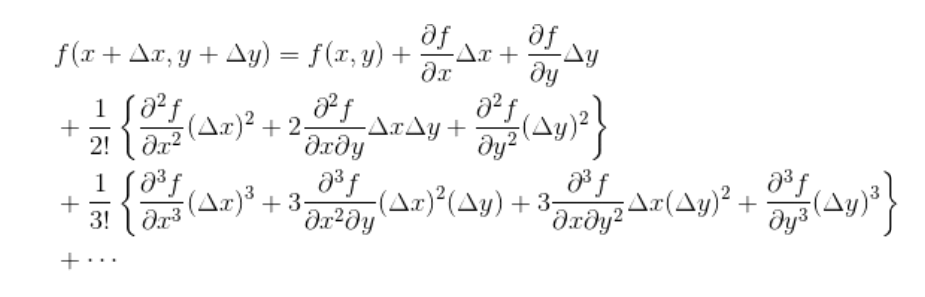
用哈密顿算子表示梯度：

$\Delta x = -\eta\nabla f$

在神经网络的世界中， $\eta$ 称为学习率。遗憾的是，它的确定方法没有明确的标准，只能通过反复试验来寻找恰当的值。

代价函数：在最优化方面，误差总和 $C_T$ 被称为误差函数、损失函数、代价函数(cost function)等。

之所以不使用误差函数(error function)、损失函数(lost function)的叫法，是因为它们的首字母容易与神经网络中用到的熵(entropy)、层(layer)的首字母混淆。

最小二乘法：平方误差的总和。

3 最优化

3-1 参数和变量

**参数：**从数学上看，神经网络是一种用于数据分析的模型，这个模型是由权重和偏置确定的。像权重和偏置这种确定数学模型的常数称为模型的参数。

确定参数的表示形式：

符号含义

$x_i$ 表示输入层(层1)的第i个神经单元的输入的变量。由于输入层的神经单元的输入和输出为同一值，所以也是表示输出的变量。此外，这个变量名也作为神经单元的名称使用

$w_{ji}^l$ 从层 l-1 的第i个神经单元指向层l的第j个神经单元的箭头的权重。请注意i和j的顺序。这是神经网络的参数

$z_j^l$ 表示层l的第j个神经单元的加权输入的变量

$b_j^l$ 层l的第j个神经单元的偏置。这是神经网络的参数

$a_j^l$ 层l的第j个神经单元的输出变量。此外，这个变量名也作为神经单元的名称使用

注意：w的下标顺序！！！这是为了矩阵与向量的乘法设计的。

符号	含义
$x_i$	表示输入层(层1)的第`i`个神经单元的输入的变量。由于输入层的神经单元的输入和输出为同一值，所以也是表示输出的变量。此外，这个变量名也作为神经单元的名称使用
$w_{ji}^l$	从层 `l-1` 的第`i`个神经单元指向层`l`的第`j`个神经单元的箭头的权重。请注意`i`和`j`的顺序。这是神经网络的参数
$z_j^l$	表示层`l`的第`j`个神经单元的加权输入的变量
$b_j^l$	层`l`的第`j`个神经单元的偏置。这是神经网络的参数
$a_j^l$	层`l`的第`j`个神经单元的输出变量。此外，这个变量名也作为神经单元的名称使用

3-2~4 变量、预测值和正解、代价函数

在固定的输入后，分清上述表格中变量之间的关系。

预测值：神经网络预测的结果，prediction。

正解：真实数据集的值，target_y。

代价函数：即预测值和正解之间的差距，追求越小越好。

Pytorch常见的Loss函数：

函数意义说明

L1Loss 计算output和target之差的绝对值 mean/sum

MSELoss 计算output和target之差的平方 mean/sum

CrossEntropyLoss 将输入经过 softmax 激活函数之后，再计算其与 target 的交叉熵损失。即该方法将 nn.LogSoftmax() 和nn.NLLLoss() 进行了结合。严格意义上的交叉熵损失函数应该是 nn.NLLLoss() 在多分类任务中，经常采用 softmax 激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要 softmax 激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算 loss。mean/sum

NLLLoss 常用于多分类任务，但是 input 在输入 NLLLoss() 之前，需要对 input 进行 log_softmax 函数激活，即将 input 转换成概率分布的形式，并且取对数。如果不想让网络的最后一层是log_softmax层的话，就可以采用 CrossEntropyLoss 完全代替此函数。mean/sum

KLDivLoss KL散度又称为相对熵 (Relative Entropy)，用于描述两个概率分布之间的差异。 KL散度值是不对称的。mean/sum

一般来说回归问题使用均方误差，或者均方根、绝对值等等，而分类问题使用交叉熵。

函数	意义	说明
L1Loss	计算output和target之差的绝对值	mean/sum
MSELoss	计算output和target之差的平方	mean/sum
CrossEntropyLoss	将输入经过 softmax 激活函数之后，再计算其与 target 的交叉熵损失。即该方法将 nn.LogSoftmax() 和nn.NLLLoss() 进行了结合。严格意义上的交叉熵损失函数应该是 nn.NLLLoss()	在多分类任务中，经常采用 softmax 激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要 softmax 激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算 loss。mean/sum
NLLLoss	常用于多分类任务，但是 input 在输入 NLLLoss() 之前，需要对 input 进行 log_softmax 函数激活，即将 input 转换成概率分布的形式，并且取对数。	如果不想让网络的最后一层是log_softmax层的话，就可以采用 CrossEntropyLoss 完全代替此函数。mean/sum
KLDivLoss	KL散度又称为相对熵 (Relative Entropy)，用于描述两个概率分布之间的差异。	KL散度值是不对称的。mean/sum

0x04 误差反向传播

梯度下降需要每一层都有明确的误差才能更新参数，所以反向传播的意义就是将输出层的误差反向传递至每一个隐藏层，用于进行权重的更新。

4-1 梯度下降回顾

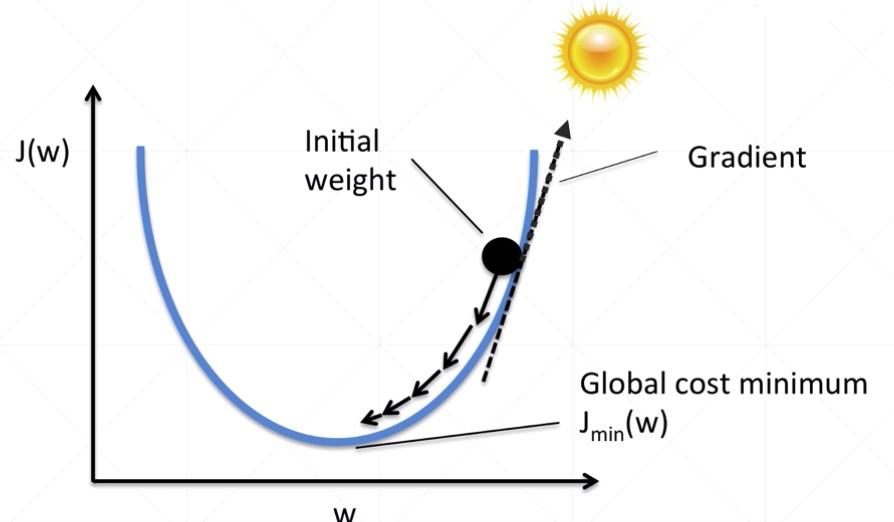
4-2 神经单元误差 $\delta_j^l$

如果神经网络符合数据，根据最小值条件，变化率应该为 0。

可以认为神经单元误差表示与符合数据的理想状态的偏差。

根据上述推导，在一般情况下：

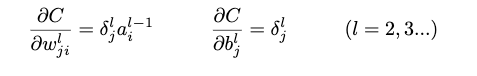
4-3 误差反向传播法

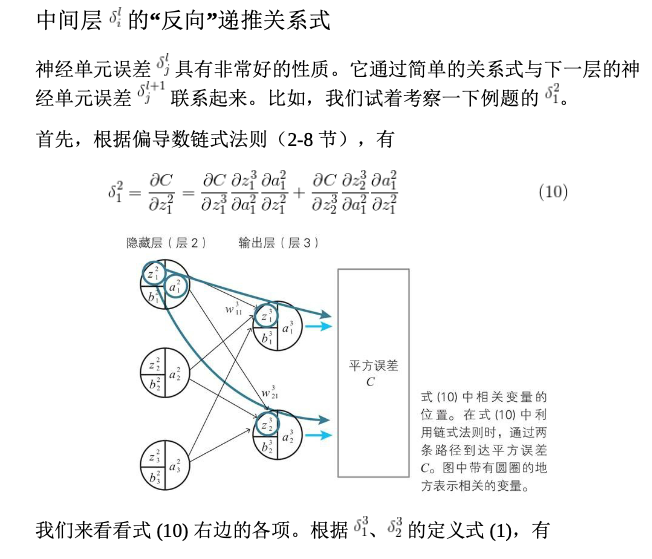
本节通过实例，说明神经单元误差符合数列的特征，可以求得末项，即输出层的单元误差；然后根据递推式，可以容易求出中间层的误差，不需要求导。

已知我们能求出输出层的误差，则中间层的推导如下（下图均截自原书）：

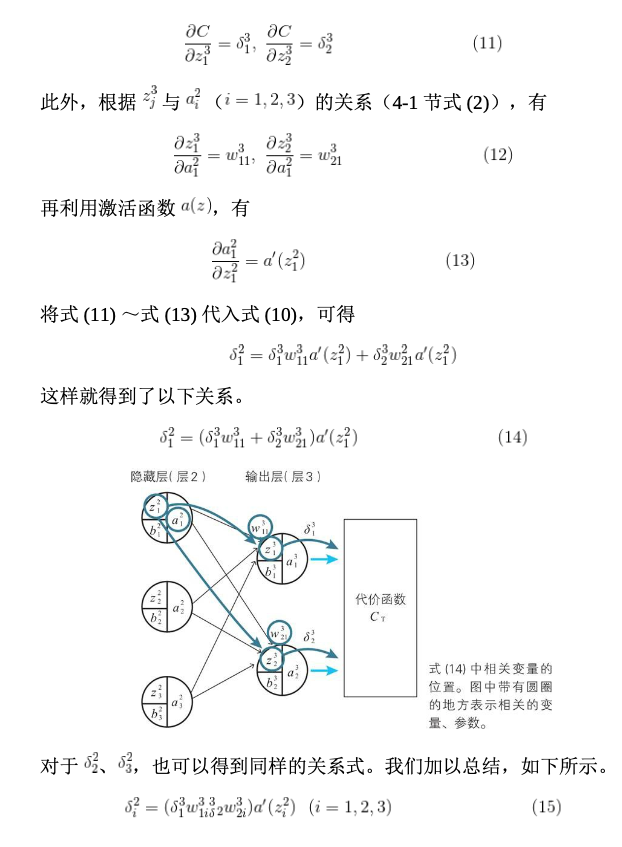
公式（15）可能存在错误，其为两项的和。

0x05 卷积神经网络

描述卷积神经网络

池化方法：

名称	说明
最大池化	使用对象区域的最大值作为代表值
平均池化	使用对象区域的平均值作为代表值
L2池化	使用对象区域的平方和的平方根作为代表值

参考：