密码学基础

教材：应用密码学 (张仕斌编著)

0x01 绪论

信息安全的基本属性：
- 真实性：确认和识别主体或资源就是其声称的。
- 保密性：信息不泄露给非授权的用户、实体和进程。
- 完整性：信息未经授权不被修改破坏。
- 可用性：保证合法用户在需求时能够获得所需的信息和相关资源。
- 可控性：可以控制授权范围内的信息流向及信息传播方式。
- 可审查性(不可否认性)：通信双方不能抵赖做出的行为。
- 可靠性：信息以用户认可的质量连续服务于用户。
信息安全机制
- 通用安全机制：可信功能、安全标签、事件检测、安全审计跟踪、安全恢复机制
- 特殊安全机制：加密、数字签名、访问控制、数据完整性、鉴别、业务流量填充、路由控制、公正机制
安全性攻击
- 被动攻击：通常采用流量监听、无线截获等方式，难以检测，需采用防止策略。
- 主动攻击：通常为伪造、重放、篡改信息和拒绝服务，主要防止途径是检测。
密码体制及其分类
- 组成：明文空间M、密文空间C、密钥空间K、加密算法E、解密算法D
- 分类：主要是对称密码体制和非对称密码体制
  
  1.密文数据段是否与明文数据段在明文的位置相观：分组密码体制与序列密码体制
  
  2.加密变换是否可逆：单向变换密码体制与双向变换密码体制
  
  3.加密过程是否引入客观随机因素：确定型密码体制和概率密码体制
评价密码体制安全性
- 评价安全性的方法：无条件安全(提供充足的资源)、计算安全性(算力不足)
- 破译原则：
  
  1.成本是否超过被加密信息本身的价值
  
  2.时间是否超过被加密信息有用的生命周期

0x02 古典密码

替换密码

单字符单表替换密码：凯撒密码、放射密码
单字符多表替换密码：维吉尼亚密码、希尔密码

换位密码

列换位：栅栏密码
周期换位

0x03 数学基础

初等数论

欧几里得算法

定理：

(说法一)设a,b,c是三个不全为0的整数，a=bq+c,其中q是整数，则(a,b)=(b,c)。

(说法二)假如a>b，且r=a mod b，那么a = kb+r，假如d是a和b的公约数，即满足d|a和d|b，r可以表示为r=a-kb，因为a和b能被d整除，那么r也能被d整除，即d|r，所以d也是b和r的公约数。

证明：

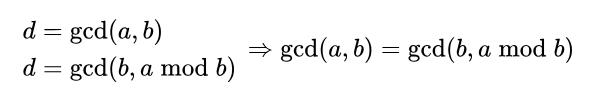
进一步辗转：

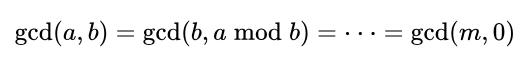
可得m是a和b的最大公约数。
欧拉定理

欧拉函数：设m为正整数，则1,2…,m中与m互素的整数个数记做φ(m)，叫做欧拉函数。

欧拉定理：设m是大于1的整数，若(a.m)=1，则 $a^{φ(m)}=1(mod m)$
费马小定理

若p为素数，a为任意正整数且不是p的倍数，则 $a^{p-1}=1(mod p)$ ==> $a^{p}=a(modp)$
离散对数

离散对数公钥加密算法安全性远高于基于大数分解的算法。

离散对数问题：给定一个素数p，g为模p循环群的原根，对任意的a， $b=g^a(modp)$ ，已知b计算a是困难的。

模重复平方算法

为了研究快速幂

//b^n mod m
//bit(n)=(nk nk-1 ...n1n0)
//list(n):n[0]=n0、n[1]=n1...
s = 1
for(i=0;i<=k;i++){
  if(n[i]==1)
    s = (s*b)%m;
  b = (b*b)%m;
}

Miller-Rabin素性检测算法

目的：基于费马小定理，用于判断模数是否是素数(伪素数)。

问题：设n为正奇数，若 $b^{n-1}=1(modn)$ 不成立，则n为合数；若成立，n也可能是合数。

内容：

群

封闭性：

$\forall a,b \in G,ab\in G$
结合律：

$\forall a,b,c \in G,a(bc)=abc \in G$
单位元：

$\forall a \in G,ae=ea=a$
逆元：

$\forall a \in G,\exists b \in G,s.t.\ ab=ba=e$

有限域

加法交换群：零元和负元
乘法交换群：单位元和逆元
乘法对加法有分配律

0x04 分组密码

安全设计原则：

分组长度足够长
密钥量足够大
密钥变换足够复杂
数据扩展足够小
差错传播尽可能小

分组密码原理：

两个基本方法：

扩散：将明文和密钥的统计特性散布到密文中去，使得明文和密钥的每一位都影响密文中多位的值。

混淆：使密文与对应的明文与密钥的统计关系尽可能的复杂

代替–置换网络（S-P结构）

S代替起到混淆的作用，P置换起到扩散的作用

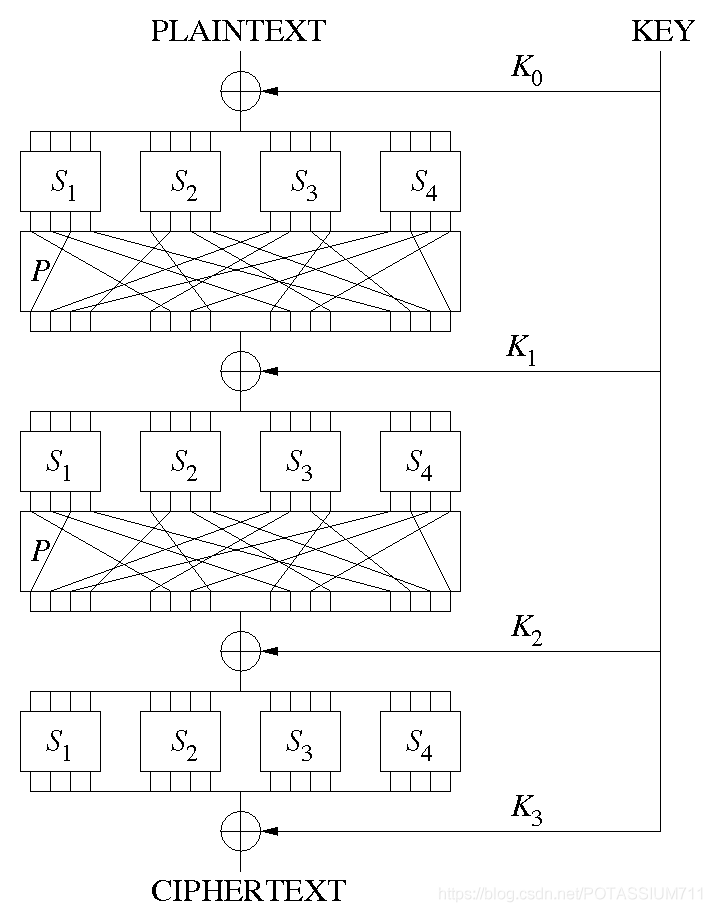
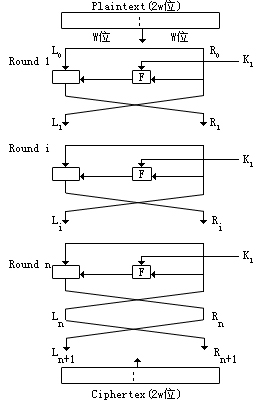
Feistel密码结构

基本过程：

$L_i=R_{i-1}$

$R_i=L_{i-1}⊕F(R_{i-1},K_i)$

保证安全性的参数：

分组大小：普遍使用64bit或128bit

密钥大小：通常128bit

轮数：一般为16

子密钥生成算法：越复杂越安全

轮函数：越复杂越安全

数据加密标准DES

1.基础知识

密钥有64bit，其中8bit是奇偶校验位，即有效密钥是56bit
轮密钥：48bit
分组：64bit
过程：16轮迭代+最后左右交换

2.轮密钥生成

若输入56bit，8位一组，末尾添加校验位(奇数校验位)。
若64bit，直接使用

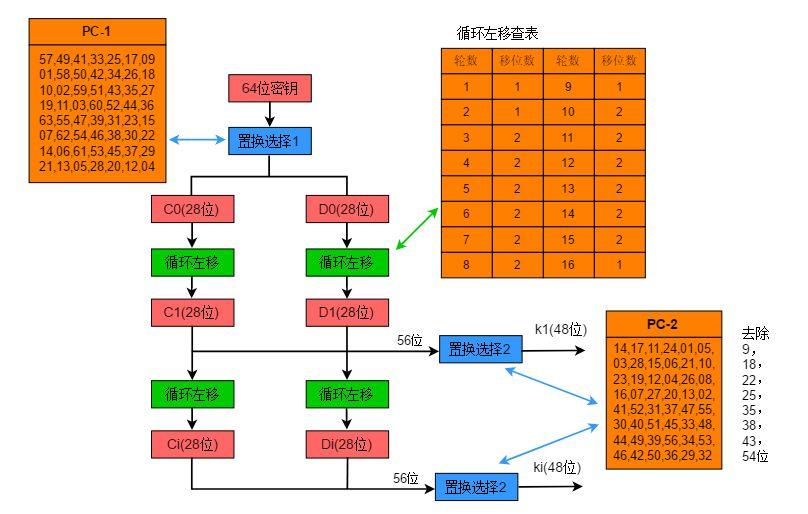
3.加密过程

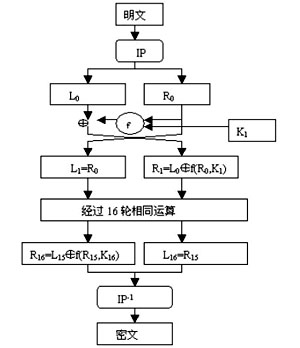
初始置换 $IP$

将64bit明文按下表重新排列输出：
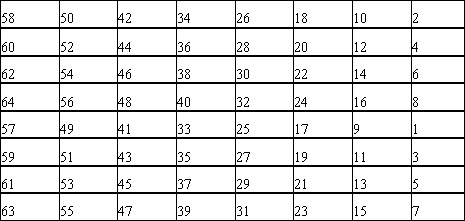
轮结构
轮结构主要过程：

F函数的主要过程：
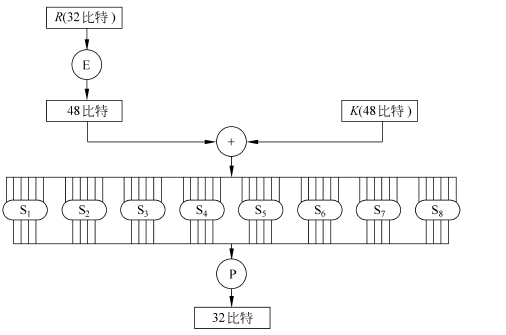
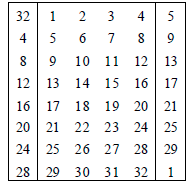
- E盒扩展：
  
  输入32位，输出48位。
- S盒代替
  
  8个S盒，输入6位 $b_5b_4b_3b_2b_1b_0$ ，输出4位；以 $b_5b_0$ 为行，以 $b_4b_3b_2b_1$ 为列，获得输出。
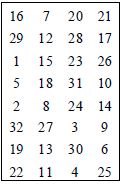
- P盒置换
  
  P盒如下：输入32位，输出32位
逆初始置换 $IP^{-1}$

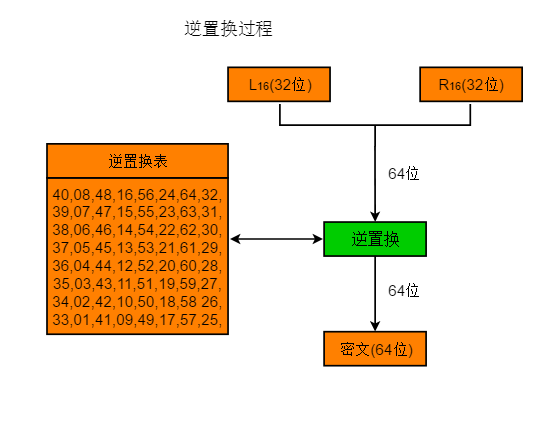
高级加密标准AES(Rijndael算法)

1.基础知识：

明文分组长度：128bit

密钥长度：128bit、192bit、256bit

基本运算：是在 $GF(2^8)$ 的有限域上进行的。

不可约多项式： $p(x)=x^8+x^4+x^3+x+1$

运算元素：一个字节(8bit)代表一个余式(256个)

加解密操作都是在一个4×4（128）的字节矩阵上完成的。

	明文列数	密钥长度	密钥矩阵(4× $N_k$ )	迭代轮数( $N_r$ )
AES-128	4（4×4）	128bit	4×4	10
AES-192	6（4×6）	192bit	4×6	12
AES-256	8（4×8）	256bit	4×8	14

2.加密过程：

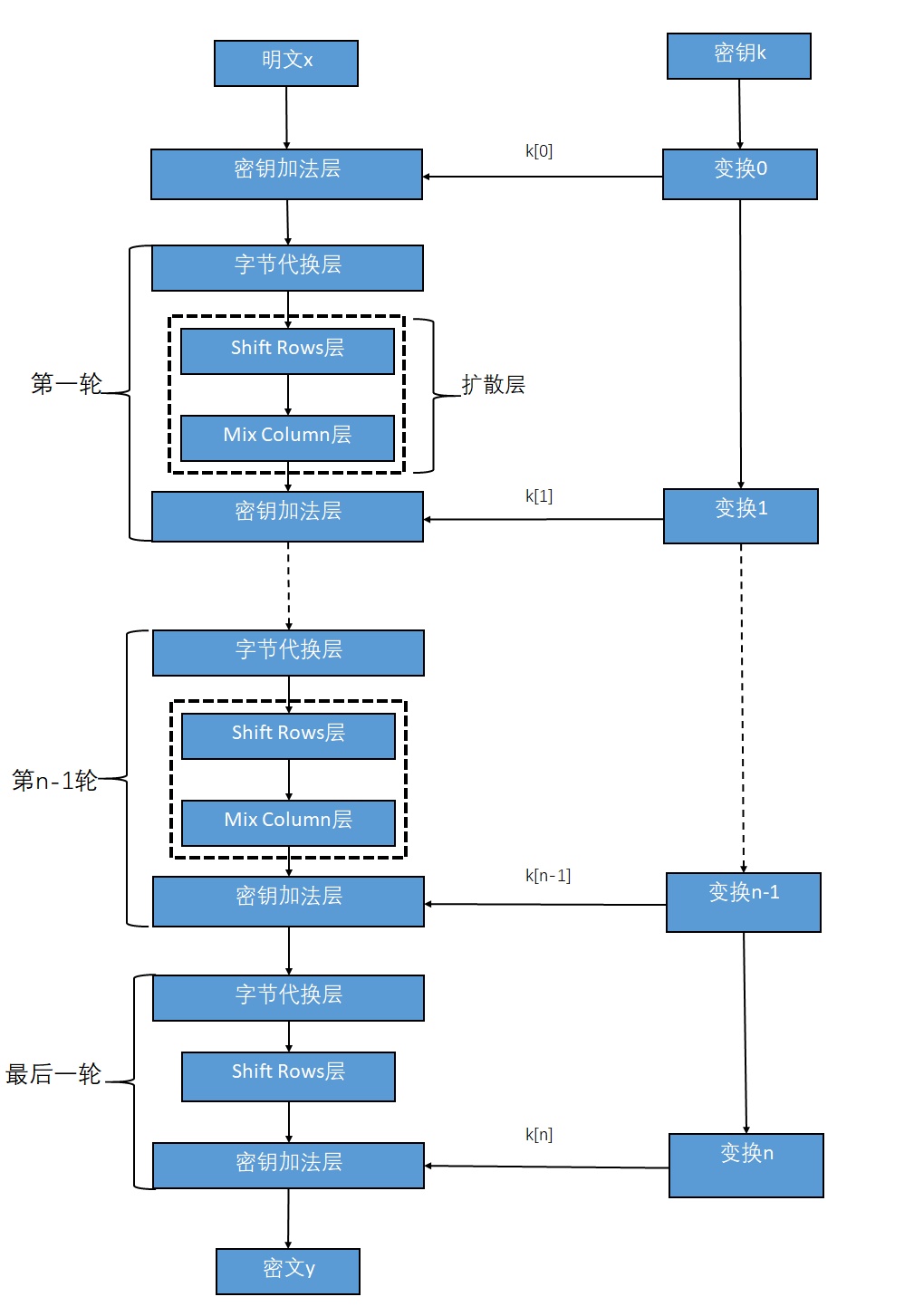
3.基本过程：

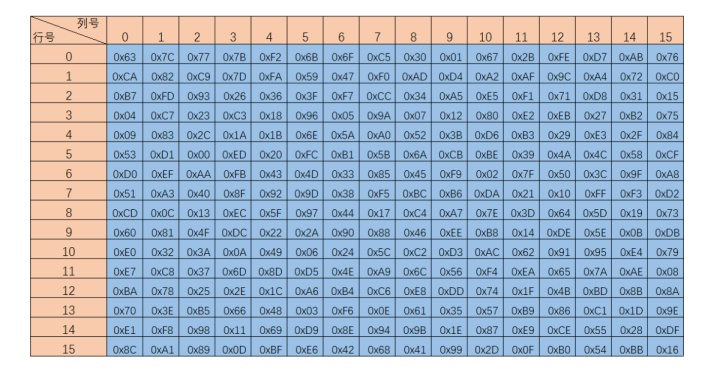
字节代替

非线性模块！

只有一个S盒，输入字节的前4位为行，后4位位列，进行查表。

SBox = {
	0:['0x63', '0x7c', '0x77', '0x7b', '0xf2', '0x6b', '0x6f', '0xc5', '0x30', '0x01', '0x67', '0x2b',  '0xfe', '0xd7', '0xab', '0x76'],
	1:['0xca', '0x82', '0xc9', '0x7d', '0xfa', '0x59', '0x47', '0xf0', '0xad', '0xd4', '0xa2', '0xaf',  '0x9c', '0xa4', '0x72', '0xc0'],
	2:['0xb7', '0xfd', '0x93', '0x26', '0x36', '0x3f', '0xf7', '0xcc', '0x34', '0xa5', '0xe5', '0xf1',  '0x71', '0xd8', '0x31', '0x15'],
	3:['0x04', '0xc7', '0x23', '0xc3', '0x18', '0x96', '0x05', '0x9a', '0x07', '0x12', '0x80', '0xe2',  '0xeb', '0x27', '0xb2', '0x75'],
	4:['0x09', '0x83', '0x2c', '0x1a', '0x1b', '0x6e', '0x5a', '0xa0', '0x52', '0x3b', '0xd6', '0xb3',  '0x29', '0xe3', '0x2f', '0x84'],
	5:['0x53', '0xd1', '0x00', '0xed', '0x20', '0xfc', '0xb1', '0x5b', '0x6a', '0xcb', '0xbe', '0x39',  '0x4a', '0x4c', '0x58', '0xcf'],
	6:['0xd0', '0xef', '0xaa', '0xfb', '0x43', '0x4d', '0x33', '0x85', '0x45', '0xf9', '0x02', '0x7f', 	'0x50', '0x3c', '0x9f', '0xa8'],
	7:['0x51', '0xa3', '0x40', '0x8f', '0x92', '0x9d', '0x38', '0xf5', '0xbc', '0xb6', '0xda', '0x21', 	'0x10', '0xff', '0xf3', '0xd2'],
	8:['0xcd', '0x0c', '0x13', '0xec', '0x5f', '0x97', '0x44', '0x17', '0xc4', '0xa7', '0x7e', '0x3d', 	'0x64', '0x5d', '0x19', '0x73'],
	9:['0x60', '0x81', '0x4f', '0xdc', '0x22', '0x2a', '0x90', '0x88', '0x46', '0xee', '0xb8', '0x14', 	'0xde', '0x5e', '0x0b', '0xdb'],
	10:['0xe0', '0x32', '0x3a', '0x0a', '0x49', '0x06', '0x24', '0x5c', '0xc2', '0xd3', '0xac', '0x62', '0x91', '0x95', '0xe4', '0x79'],
	11:['0xe7', '0xc8', '0x37', '0x6d', '0x8d', '0xd5', '0x4e', '0xa9', '0x6c', '0x56', '0xf4', '0xea', '0x65', '0x7a', '0xae', '0x08'],
	12:['0xba', '0x78', '0x25', '0x2e', '0x1c', '0xa6', '0xb4', '0xc6', '0xe8', '0xdd', '0x74', '0x1f', '0x4b', '0xbd', '0x8b', '0x8a'],
	13:['0x70', '0x3e', '0xb5', '0x66', '0x48', '0x03', '0xf6', '0x0e', '0x61', '0x35', '0x57', '0xb9', '0x86', '0xc1', '0x1d', '0x9e'],
	14:['0xe1', '0xf8', '0x98', '0x11', '0x69', '0xd9', '0x8e', '0x94', '0x9b', '0x1e', '0x87', '0xe9', '0xce', '0x55', '0x28', '0xdf'],
	15:['0x8c', '0xa1', '0x89', '0x0d', '0xbf', '0xe6', '0x42', '0x68', '0x41', '0x99', '0x2d', '0x0f', '0xb0', '0x54', '0xbb', '0x16']
}

行移位

作用于S盒的输出。

每行进行循环左移，左移距离：与列数和所在行相关。

$N_b$	$C_1$	$C_2$	$C_3$
4	1	2	3
6	1	2	3
8	1	3	4

列混合

将状态矩阵的每列与一固定的多项式 $a(x)$ 相乘(在域 $GF(2^8)$ 上运算)，然后模多项式 $x^4+1$ 。

其中 $a(x)=\{03\}x^3+\{01\}x^2+\{01\}x+\{02\}$ （其中一个）:

输入：状态矩阵 $B$

输出：矩阵 $C$

$C=A_{4×4}B$

其中：

$A_{4×4}=\left[ \begin{matrix} 02&03&01&01\\ 01&02&03&01\\ 01&01&02&03\\ 03&01&01&02\\ \end{matrix} \right]$
轮密钥加
- 状态矩阵与轮密钥矩阵对应位置进行异或( $xor$ )运算。
- 密钥扩展过程（以 $N_k=4$ 为例）：
  
  第 $i$ 列密钥的生成：
  
  $K_i=\left\{ \begin{array}{} K_{i-4}\oplus K_{i-1},\ (if\ i\ mod4\ !=0)\\ K_{i-4}\oplus T(K_{i-1}),\ (if\ i\ mod4\ =0)\\ \end{array} \right.$
  
  函数 $T(K_{i-1})$ :
  - 将 $K_{i-1}$ 以字节形式左移一位：FFEEEEAA ==> EEEEAAFF
  - 将左移后的进行字节替换(S盒)
  - 将结果与 $Rcon[i/N_k]$ 进行异或

i	$RC$	$Rcon$
1	01	01000000
2	02	02000000
3	04	04000000
4	08	08000000
5	10	10000000
6	20	20000000
7	40	40000000
8	80	80000000
9	1B	1B000000
10	36	36000000

其中 $RC[i]=x^{i-1}$

0x05 序列密码*

0x06 非对称密码

RSA

密钥生成

1.选择两个大素数p,q.计算 $n=pq,\varphi(n)=(p-1)(q-1)$ 。

2.选择一个整数 $e,1<e<\varphi(n),gcd(\varphi(n),e)=1$ 。通过 $de=1mod\varphi(n)$ 计算得到d。

3.{e,n}为公钥，{d,n}为私钥。
加密算法

消息m，计算 $c=m^e(modn)$
解密算法

计算 $m=c^d(modn)$

ELGamal

密钥生成：

令 $g\in Zp*$ 是一个本原元，选择 $x,1<x<p-1$ ,计算 $y=g^xmodp$ ， ${g,y,p}$ 是公钥， ${g,x,p}$ 是私钥。
加密算法：

对于消息m，发送方随机选择秘密 $k,1<k<p$ ，计算 $C_1=g^kmodp,C_2=my^kmodp$ ，发送 $C_1,C_2$ 。
解密算法：

计算 $C_1^{-x}C_2modp=m$ ，即为发送方的消息m。

0x07 认证–Hash函数

Hash函数是一个公开函数，不需要密钥，用于将任意长的消息m映射为较短的、固定长度的一个值H(m)。

对H的六个要求：

能够接受任意长度的消息作为输入

能够生成较短的、固定长度的输出

对任何消息输入都应该能够容易快速地计算出哈希值

单向性：H(m)不能恢复出m

抵抗弱碰撞：给定消息m和H(m)，找到 m'!= m 使得 H(m)=H(m')是不可能的

抵抗强冲突：可以有两个有意义的消息m和m’，使得 H(m)=H(m')是不可能的

0x08 认证–数字签名

典型数字签名方案

RSA

条件：{e,n}为公钥，{d,n}为私钥，信息为m

签名过程： $s=m^d(modn)$

验证过程： $m=s^e(modn)$ 是否成立

缺点：都次使用同一个密钥签名，会出现 $m=m1*m2$ ,其中m为恶意构造的信息

改进：对H(m)进行签名
ElGamal

条件： $y=g^x(modp)$ , ${g,y,p}$ 为公钥， ${g,x,p}$ 为私钥，信息为m

签名过程：签名者随机选择秘密k，计算 $\gamma=g^k(modp),\delta=(m-x\gamma)k^{-1}mod(p-1)$ ，其中 $(m,\gamma,\delta)$ 为对消息m的签名。

验证过程： $y^{\gamma}\gamma^{\delta}modp=g^m(modp)$ 是否成立

盲签名方案

基于大数分解问题

过程如下：
基于离散对数难题

过程如下：